本文共 7415 字，大约阅读时间需要 24 分钟。

尼姆博弈

题型

尼姆博弈模型：

有3堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取1个，多者不限，最后取光者得胜。

分析

首先自己想一下，就会发现只要最后剩两堆物品一样多(不为零)，第三堆为零，那面对这种局势的一方就必败。那我们用(a,b,c)表示某种局势，首先(0,0,0)显然是必败态，无论谁面对(0,0,0) ，都必然失败；第二种必败态是(0,n,n)，自己在某一堆拿走k（k ≤ n）个物品，不论k为多少，对方只要在另一堆拿走k个物品，最后自己都将面临(0,0,0)的局势，必败。仔细分析一下，(1,2,3)也是必败态，无论自己如何拿，接下来对手都可以把局势变为(0,n,n)的情形。

可以用符号XOR表示这种运算，这种运算和一般加法不同的一点是1 XOR 1 = 0。先看(1,2,3)的按位模2加的结果： 1 = 二进制01 2 = 二进制10 3 = 二进制11 XOR 0 = 二进制00 (注意不进位) 对于奇异局势(0,n,n)也一样，结果也是0 任何奇异局势(a,b,c)都有a XOR b XOR c = 0

如果我们面对的是一个非必败态(a,b,c)，要如何变为必败态呢？

假设 a < b < c，我们只要将 c 变为a XOR b，即可。

推广

有n堆若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

这个游戏中的变量是堆数k和各堆的物品数N1，N2，……，Nk。 对应的组合问题是，确定先手获胜还是后手获胜以及两个游戏人应该如何取物品才能保证自己获胜。

首先回忆一下，每个正整数都有对应的一个二进制数，例如：57(10) = 111001(2) ，即：57(10)=2⁵+2⁴+2³+2⁰。于是，我们可以认为每一堆物品数由2的幂数的子堆组成。这样，含有57枚物品大堆就能看成是分别由数量为=2⁵+2⁴+2³+2⁰的各个子堆组成。

现在考虑各大堆大小分别为N1，N2，……Nk的一般的Nim博弈。将每一个数Ni表示为其二进制数（数的位数相等，不等时在前面补0）：

N1 = as…a1a0 N2 = bs…b1b0 …… Nk = ms…m1m0 如果每一种大小的子堆的个数都是偶数，我们就称Nim博弈是平衡的，而对应位相加是偶数的称为平衡位，否则称为非平衡位。因此，Nim博弈是平衡的，当且仅当： as +bs + … + ms 是偶数，即as XOR bs XOR … XOR ms = 0 …… a1 +b1 + … + m1 是偶数，即a1 XOR b1 XOR … XOR m1 = 0 a0 +b0 + … + m0是偶数，即a0 XOR b0 XOR … XOR m0 = 0

于是，我们就能得出尼姆博弈中先手获胜策略：

Bouton定理：先手能够在非平衡尼姆博弈中取胜，而后手能够在平衡的尼姆博弈中取胜。即状态(x1, x2, x3, …, xn)为P状态当且仅当x1 xor x2 xor x3 xor … xor xn =0。这样的操作也称为Nim和(Nim Sum) 我们以一个两堆物品的尼姆博弈作为试验。设游戏开始时游戏处于非平衡状态。这样，先手就能通过一种取子方式使得他取子后留给后手的是一个平衡状态下的游戏，接着无论后手如何取子，再留给先手的一定是一个非平衡状态游戏，如此反复进行，当后手在最后一次平衡状态下取子后，先手便能一次性取走所有的物品而获胜。而如果游戏开始时游戏牌平衡状态，那根据上述方式取子，最终后手能获胜。

下面应用此获胜策略来考虑4堆的Nim博弈。其中各堆的大小分别为7，9，12，15枚硬币。用二进制表示各数分别为：0111，1001，1100和1111

于是可得到如下一表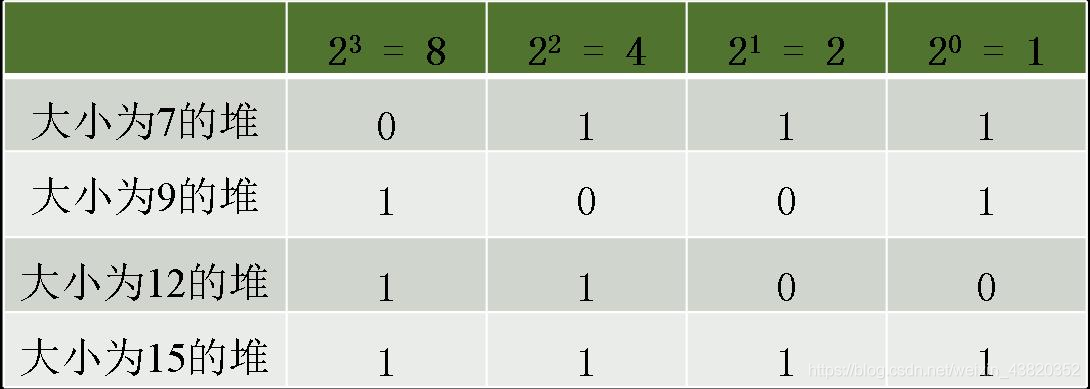： 由Nim博弈的平衡条件可知，此游戏是一个非平衡状态的Nim博弈，因此，先手在按获胜策略一定能够取得最终的胜利。具体做法有多种，先手可以从大小为12的堆中取走11枚硬币，使得游戏达到平衡（如下表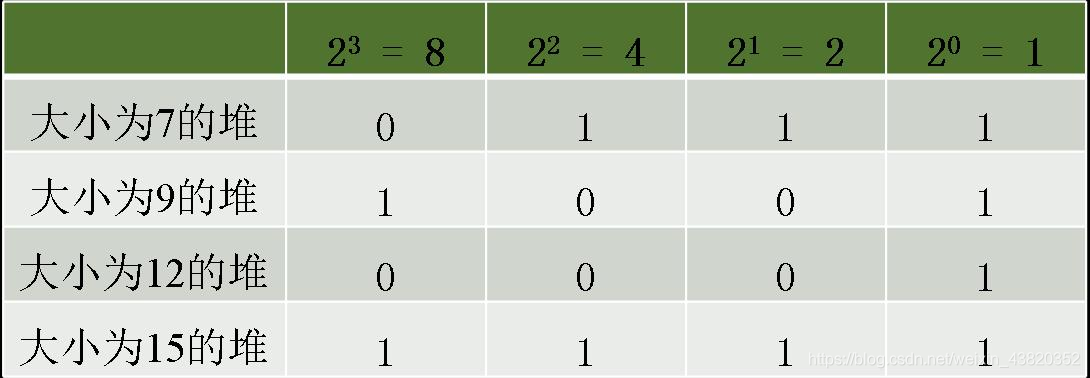） 之后，无论后手如何取子，先手在取子后仍使得游戏达到平衡。

同样的道理，先手也可以选择大小为9的堆并取走5枚硬币而剩下4枚，或者，先手从大小为15的堆中取走13枚而留下2枚。

归根结底， Nim博弈的关键在于游戏开始时游戏处于何种状态（平衡或非平衡）和先手是否能够按照取子游戏的获胜策略来进行游戏。当堆数大于2时，Bouton定理依旧适用。

例题

下面是一个二人小游戏：桌子上有M堆扑克牌；每堆牌的数量分别为Ni(i=1…M)；两人轮流进行；每走一步可以任意选择一堆并取走其中的任意张牌；桌子上的扑克全部取光，则游戏结束；最后一次取牌的人为胜者。

现在我们不想研究到底先手为胜还是为负，我只想问大家： ——“先手的人如果想赢，第一步有几种选择呢？”

Input

输入数据包含多个测试用例，每个测试用例占2行，首先一行包含一个整数M(1<M<=100)，表示扑克牌的堆数，紧接着一行包含M个整数Ni(1<=Ni<=1000000，i=1…M)，分别表示M堆扑克的数量。M为0则表示输入数据的结束。

Output

如果先手的人能赢，请输出他第一步可行的方案数，否则请输出0，每个实例的输出占一行。

Sample Input

3 5 7 9 0

Sample Output

1

# include 
   
    using namespace std;int main() {
       int nPile, i, sum, cnt;    int p[105];    while (scanf("%d", &nPile) && nPile) {
           cnt = 0;        sum = 0;        for (i = 0; i < nPile; i++) {
               scanf("%d", &p[i]);            sum ^= p[i];        }        for (i = 0; i < nPile; i++) {
               if (p[i] > (sum ^ p[i]))//注意'^'的优先级小于'>'                cnt++;        }        printf("%d\n", cnt);    }    return 0;}
   

SG函数

组合游戏

在竞赛中，组合游戏的题目一般有以下特点：

题目描述一般为A、B 2人做游戏 A、B交替进行某种游戏规定的操作，每操作一次，选手可以在有限的操作（操作必须合法）集合中任选一种。 对于游戏的任何一种可能的局面，合法的操作集合只取决于这个局面本身，不取决于其它因素（跟选手，以前的所有操作无关）。 如果当前选手无法进行合法的操作，则为负。

SG函数

先定义mex(minimal excludant)运算，这是施加于一个集合的运算，表最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。

对于任意状态 x ， 定义 SG(x) = mex(S),其中 S 是 x 后继状态的 SG 函数值的集合。如 x 有三个后继状态分别为 SG(a)，SG(b)，SG©，那么=mexSG(x)=mex{SG(a),SG(b),SG©}。 这 集合S的终态必然是空集，所以SG函数的终态为 SG(x)=0，当且仅当 x 为必败点P时。

取石子问题

有1堆n个的石子，每次只能取{ 1, 3, 4 }个石子，先取完石子者胜利，那么各个数的SG值为多少？

SG[0]=0，f[]={1,3,4}, x=1 时，可以取走1 - f{1}个石子，剩余{0}个，所以 SG[1] = mex{ SG[0] }= mex{0} = 1; x=2 时，可以取走2 - f{1}个石子，剩余{1}个，所以 SG[2] = mex{ SG[1] }= mex{1} = 0; x=3 时，可以取走3 - f{1,3}个石子，剩余{2,0}个，所以 SG[3] = mex{SG[2],SG[0]} = mex{0,0} =1; x=4 时，可以取走4- f{1,3,4}个石子，剩余{3,1,0}个，所以 SG[4] = mex{SG[3],SG[1],SG[0]} = mex{1,1,0} = 2; x=5 时，可以取走5 - f{1,3,4}个石子，剩余{4,2,1}个，所以SG[5] = mex{SG[4],SG[2],SG[1]} =mex{2,0,1} = 3; 以此类推…

x 0 1 2 3 4 5 6 7 8…

SG[x] 0 1 0 1 2 3 2 0 1…

由上述实例我们就可以得到SG函数值求解步骤，那么计算1~n的SG函数值步骤如下：

1、使用 数组f 将 可改变当前状态 的方式记录下来。 2、然后我们使用 另一个数组 将当前状态x 的后继状态标记。 3、最后模拟mex运算，也就是我们在标记值中 搜索 未被标记值 的最小值，将其赋值给SG(x)。 4、我们不断的重复 2 - 3 的步骤，就完成了 计算1~n 的函数值。

代码：

#include 
   
    #include 
    
     #define ll long longusing namespace std;// N 可选择的种类数为N+1种const int N = 2;const int MAXN = 110;// f[N]:可改变当前状态的方式，N为方式的种类，f[N]要在getSG之前先预处理// SG[]:0~n的SG函数值// S[]:为x后继状态的集合int f[N], SG[MAXN], S[MAXN];void getSG(int n) {
       int i, j;    memset(SG, 0, sizeof(SG));    //因为SG[0]始终等于0，所以i从1开始    for (i = 1; i <= n; i++) {
           //每一次都要将上一状态 的 后继集合 重置        memset(S, 0, sizeof(S));        for (j = 0; f[j] <= i && j <= N; j++) {
               S[SG[i - f[j]]] = 1;  //将后继状态的SG函数值进行标记        }        for (j = 0;; j++) {
               if (!S[j]) {
      //查询当前后继状态SG值中最小的非零值                SG[i] = j;                break;            }        }    }}int main() {
       f[0]=1;    f[1]=3;    f[2]=4;    getSG(100);    for (int i = 0; i <= 100; i++) {
           cout << SG[i] << " ";    }    return 0;}
    
   

SG模版（要根据题目修改SG的模版）

// N 可选择的种类数为N+1种const int N = 2;const int MAXN = 110;// f[N]:可改变当前状态的方式，N为方式的种类，f[N]要在getSG之前先预处理// SG[]:0~n的SG函数值// S[]:为x后继状态的集合int f[N], SG[MAXN], S[MAXN];void getSG(int n) {
       int i, j;    memset(SG, 0, sizeof(SG));    // 因为SG[0]始终等于0，所以i从1开始    for (i = 1; i <= n; i++) {
           // 每一次都要将上一状态的后继集合重置        memset(S, 0, sizeof(S));        // 将后继集合中出现的数进行标记        for (j = 0; f[j] <= i && j <= N; j++) {
               S[SG[i - f[j]]] = 1;        }        // 查询当前后继状态SG值中最小的非零值        for (j = 0;; j++) {
               if (!S[j]) {
                   SG[i] = j;                break;            }        }    }}

对于不同的题目可能需要递归进行标记后继集合中的数。

例如：51nod 1714 B君的游戏 B君和L君要玩一个游戏。刚开始有n个正整数 𝑎𝑖 。

双方轮流操作。每次操作，选一个正整数x，将其移除，再添加7个数字 𝑥1,𝑥2…𝑥7 。要求对于 𝑥𝑖 ，满足 0<=𝑥𝑖<𝑥 且 𝑥&𝑥𝑖=𝑥𝑖

注意0不能被选取，所以这个游戏一定会结束，而谁无法操作谁就失败。

B君根据自己的经验，认为先手胜率高一点，所以B君是先手。 B君想知道自己是否必胜。

#include 
   
    #include 
    
     #include 
     
      #define ll unsigned long longusing namespace std;const int maxn = 70000000;int sg[65] = {
   0, 1, 2, 4, 8, 16, 32, 64, 128, 255, 256, 512,              1024, 2048, 3855, 4096, 8192, 13107, 16384, 21845,              27306, 32768, 38506, 65536, 71576, 92115, 101470,              131072, 138406, 172589, 240014, 262144, 272069,              380556, 524288, 536169, 679601, 847140, 1048576,              1072054, 1258879, 1397519, 2005450, 2097152, 2121415,              2496892, 2738813, 3993667, 4194304, 4241896, 4617503,              5821704, 7559873, 8388608, 8439273, 8861366, 11119275,              11973252, 13280789, 16777216, 16844349, 17102035,              19984054, 21979742, 23734709};//int vis[maxn];//yu控制递归层数，cur控制所分配最大值，ans，控制最终分配值，next控制所分配最小值//void dfs(int cur, int yu, int ans, int next) {
   //    if (yu == 0) {
   //        vis[ans] = 1;//        return;//    }//    for (int i = next; i < cur; i++) {
   //        dfs(cur, yu - 1, ans ^ sg[i], i);//    }//}////void getSG() {
   //    memset(sg, 0, sizeof(sg));//    for (int i = 1; i <= 64; i++) {
   //        memset(vis, 0, sizeof(vis));//        dfs(i, 7, 0, 0);//        for (int j = 0;; j++) {
   //            if (!vis[j]) {
   //                sg[i] = j;//                break;//            }//        }//        printf("%d\n", sg[i]);//    }//}int cal(ll x) {
       int num = 0;    for (int i = 0; i < 64; i++) {
           if ((x >> i) & 1) {
               num++;        }    }    return num;}int main() {
   //    getSG();    int n;    while (cin >> n) {
           ll ans = 0;        for (ll i = 1; i <= n; i++) {
               ll use;            cin >> use;            ans ^= sg[cal(use)];        }        if (ans == 0) {
               printf("L\n");        } else {
               printf("B\n");        }    }    return 0;}
     
    
   

参考博客

转载地址：https://blog.csdn.net/weixin_43820352/article/details/112979459 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！