
本文共 9921 字,大约阅读时间需要 33 分钟。
目录
在上次KNN算法中,其中有个K值,只是随机取了一个数值来了解这个KNN算法的基本流程,那这个K值怎么取会得到的模型最好呢?就涉及到模型的选择与调优来接近这个问题
1.超参数搜索
像刚才提到的KNN中的k值、决策树的树的数量或深度等,我们在使用这些算法的时候,都需要人工设定的参数,称为超参数。每改变一次超参数,模型则需要重新训练。
而参数就是在训练模型中学习到一部分,比如回归系统、神经网络等,是通过模型训练获得的。
对于超参数的设定,如果人工设置过程比较复杂,所以利用网络搜索、随机搜索、贝叶斯优化算法来寻找这个最优参数。
2.超参数调优过程
一般过程为:
1)将数据集划分为训练集、验证集、测试集
2)选择模型性能评价指标
3)用训练集对模型进行训练
4)在验证集上对模型进行参数搜索,用性能指标来评价参数好坏
5)选出最优参数
3.网络搜索
Grid Search。对模型预设几种超参数组合,选出表现最好的参数,也称为暴力搜索。
为避免初始数据的划分对结果的影响,采用交叉验证来减少偶然性,一般交叉验证和网格搜索来配合使用得到最优参数。
原理
在一定区间内,循环遍历,尝试每一种可能性,并计算其约束函数和目标函数的值,对满足条件的点,逐个比较其目标函数的值,抛弃坏点,保留好点,最终得到最优解的近似解。
交叉验证
cross validation
在上次介绍KNN的时候在训练模型的时候将数据集分成了训练集和测试集,那对于交叉验证就是将训练集在进行分成训练集和验证集。
我们可以将训练集分成4份,其中一份最为验证集。经过四次验证,每次都更换不同的验证集,即取得4组模型的结果,取平均值作为最终结果。数据分成几份就称为几折交叉验证,像分成4份,则称为4折验证
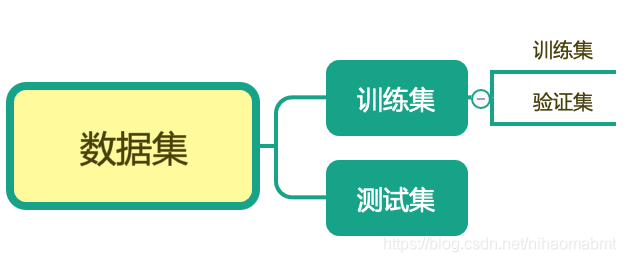
该目的就是让评估模型更加准确。
对应的sklearn 的API
sklearn.model-selection.GridSearchCV(estimator, param_grid, scoring=None, n_jobs=None, iid='warn', refit=True, cv='warn', verbose=0, pre_dispatch='2*n_jobs', error_score='raise-deprecating', return_train_score=False)
其中参数如下:
| 参数 | 含义 |
| estimator | 实例化的预估器 |
| param_grid | 预估参数,以字典的形式传入("n_neighbors":[1,3,5]) |
| scoring | 准确度的评价指标,默认的为None,使用的是score函数 也可以设置其他评价指标,如scoring=‘roc_auc’ |
| n_jobs | 并行数,默认为1,-1表示与CPU核数一致 |
| iid | 默认为各个样本fold概率分布一致 |
| refit | 默认为True:程序会以交叉验证训练集得到最佳参数 |
| cv | 几折交叉验证,数据量大的时候,该值稍微小点 |
| verbose | 日志容长度,默认为0:不输出训练过程;1:偶尔输出;>1每个子模型都输出 |
| pre_dispatch | 指定总共分发的并行任务数。当n_jobs>1时,数据在每个运行点进行复制 |
| error_socre | 默认为raise-deprecating:在模型拟合过程中如果产生误差,误差分数会提高 numeric:如果产生误差,fitfailed warning会提高 |
| return_train_score | 默认为True:交叉验证结果中包含训练得分 |
返回值仍为预估器,返回值里面的参数如下:
| 返回值 | 含义 |
| best_params | 最佳参数 |
| best_score | 最佳结果 |
| best_estimator | 最佳预估器 |
| cv_results | 交叉验证结果 |
实例
结合上次总结的中提到的给鸢尾花分类的例子,增加网格搜索的方式来进行选择k值。
def knn_iris_gscv(): #添加网格搜索和交叉验证 #用knn进行分类 # 从sklearn.datasets中获取到鸢尾花的数据集,使用load_*方法说明是一个比较小的数据集 iris = load_iris() # 数据分成训练集和测试集 x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=10) # 为防止数据量级差别比较大,所以将数据进行无量纲化,这里采用标准化 standard = StandardScaler() x_train = standard.fit_transform(x_train) x_test = standard.fit_transform(x_test) # 为防止数据量级差别比较大,所以将数据进行无量纲化,这里采用标准化 standard = StandardScaler() x_train = standard.fit_transform(x_train) x_test = standard.fit_transform(x_test) # 传入到knn进行训练,得到模型 classifier = KNeighborsClassifier() param_dict = {"n_neighbors":[1,3,5,7,9]} #加入网格搜索和交叉验证 classifier = GridSearchCV(classifier,param_grid=param_dict,cv=4) classifier.fit(x_train,y_train) y_predict = classifier.predict(x_test) print("最佳参数 :",classifier.best_params_) print("最佳结果:",classifier.best_score_) print("最佳预估器:",classifier.best_estimator_) print("交叉验证结果",classifier.cv_results_) print("准确度为:", classifier.score(x_test,y_test)) return None 看下运行结果:
最佳参数 : {'n_neighbors': 7}最佳结果: 0.9333333333333333最佳预估器: KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=7, p=2, weights='uniform')交叉验证结果 {'mean_fit_time': array([0.00062317, 0.00055081, 0.00054991, 0.00055623, 0.00057566]), 'std_fit_time': array([7.58426654e-05, 4.64360734e-05, 3.64887543e-05, 3.29138554e-05, 5.62770125e-05]), 'mean_score_time': array([0.00291884, 0.00281823, 0.00283533, 0.00278461, 0.00289708]), 'std_score_time': array([2.21179304e-04, 1.79146338e-04, 9.36839974e-05, 9.96620318e-05, 4.34642939e-05]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9], mask=[False, False, False, False, False], fill_value='?', dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}], 'split0_test_score': array([0.90322581, 0.90322581, 0.90322581, 0.96774194, 0.96774194]), 'split1_test_score': array([0.9, 0.9, 0.9, 0.9, 0.9]), 'split2_test_score': array([0.83333333, 0.86666667, 0.86666667, 0.86666667, 0.83333333]), 'split3_test_score': array([0.93103448, 0.96551724, 0.96551724, 1. , 0.96551724]), 'mean_test_score': array([0.89166667, 0.90833333, 0.90833333, 0.93333333, 0.91666667]), 'std_test_score': array([0.03573672, 0.03533239, 0.03533239, 0.05261955, 0.05528267]), 'rank_test_score': array([5, 3, 3, 1, 2], dtype=int32)}准确度为: 0.9 我们可以看到当k值取到7时,分类效果最佳。
4.随机搜索
Random Search。利用随机数去求函数近似的最优解的方法。
原理
在一定区间内,不断随机产生随机点,并计算约束函数和目标函数的值,对满足条件的点,逐个比较其目标函数的值,抛弃坏点,保留好点,最终得到最优解的近似解。
所取的概率点越多,则得到的最优解的概率越高。
效率要高于网格搜索。
对应的sklearn的API
sklearn.model-selection.RandomizedSearchCV(estimator, param_distributions, n_iter=10, scoring=None, n_jobs=None, iid='warn', refit=True, cv='warn', verbose=0, pre_dispatch='2*n_jobs', random_state=None, error_score='raise-deprecating', return_train_score=False)
其中参数如下:
| 参数 | 含义 |
| estimator | 实例化的预估器 |
| param_distributions | 字典或列表,需要优化的参数的取值范围 |
| n_iter | 抽样参数,默认为10 |
| scoring | 准确度的评价指标,默认的为None,使用的是score函数 也可以设置其他评价指标,如scoring=‘roc_auc’ |
| n_jobs | 并行数,默认为1,-1表示与CPU核数一致 |
| iid | 默认为各个样本fold概率分布一致 |
| refit | 默认为True:程序会以交叉验证训练集得到最佳参数 |
| cv | 几折交叉验证,数据量大的时候,该值稍微小点 |
| verbose | 日志容长度,默认为0:不输出训练过程;1:偶尔输出;>1每个子模型都输出 |
| pre_dispatch | 指定总共分发的并行任务数。当n_jobs>1时,数据在每个运行点进行复制 |
| random_state | 随机种子。 默认为None:np.random所使用的随机状态实例 int值:随机状态是随机数生成器所使用的种子; 随机实例:随机状态是随机数生成器 |
| error_socre | 默认为raise-deprecating:在模型拟合过程中如果产生误差,误差分数会提高 numeric:如果产生误差,fitfailed warning会提高 |
| return_train_score | 默认为True:交叉验证结果中包含训练得分 |
参数大多数和网格搜索的类似,返回值同网格搜索。
实例
实例还是上次提到的鸢尾花的分类,其实唯一区别的就是将GridSearchCV换成了RandomizedSearchCV
from sklearn.model_selection import RandomizedSearchCVdef knn_iris_random(): # 用knn进行分类 # 从sklearn.datasets中获取到鸢尾花的数据集,使用load_*方法说明是一个比较小的数据集 iris = load_iris() # 数据分成训练集和测试集 x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=10) # 为防止数据量级差别比较大,所以将数据进行无量纲化,这里采用标准化 standard = StandardScaler() x_train = standard.fit_transform(x_train) x_test = standard.fit_transform(x_test) # 为防止数据量级差别比较大,所以将数据进行无量纲化,这里采用标准化 standard = StandardScaler() x_train = standard.fit_transform(x_train) x_test = standard.fit_transform(x_test) # 传入到knn进行训练,得到模型 classifier = KNeighborsClassifier() param_dict = {"n_neighbors": range(1,10,2)} # 加入网格搜索和交叉验证 classifier = RandomizedSearchCV(classifier, param_distributions=param_dict, cv=8) classifier.fit(x_train, y_train) y_predict = classifier.predict(x_test) print("最佳参数 :", classifier.best_params_) print("最佳结果:", classifier.best_score_) print("最佳预估器:", classifier.best_estimator_) print("交叉验证结果", classifier.cv_results_) print("准确度为:", classifier.score(x_test, y_test)) return None 输出的结果如下:
最佳参数 : {'n_neighbors': 7}最佳结果: 0.9583333333333334最佳预估器: KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=7, p=2, weights='uniform')交叉验证结果 {'mean_fit_time': array([0.00036195, 0.00031918, 0.00031105, 0.00030887, 0.00031501]), 'std_fit_time': array([3.97733068e-05, 1.15625330e-05, 9.55158621e-06, 8.84802795e-06, 2.12870376e-05]), 'mean_score_time': array([0.0011453 , 0.00108483, 0.00104901, 0.00105032, 0.00106758]), 'std_score_time': array([9.20791837e-05, 6.29039349e-05, 2.34934375e-05, 2.43233512e-05, 4.40424282e-05]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9], mask=[False, False, False, False, False], fill_value='?', dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}], 'split0_test_score': array([1. , 0.9375, 0.9375, 1. , 1. ]), 'split1_test_score': array([0.8125, 0.8125, 0.8125, 0.875 , 0.875 ]), 'split2_test_score': array([0.9375, 0.9375, 0.9375, 0.9375, 0.9375]), 'split3_test_score': array([0.93333333, 0.93333333, 0.93333333, 0.93333333, 0.93333333]), 'split4_test_score': array([1., 1., 1., 1., 1.]), 'split5_test_score': array([0.85714286, 0.85714286, 0.85714286, 0.92857143, 0.92857143]), 'split6_test_score': array([1. , 1. , 0.92857143, 1. , 1. ]), 'split7_test_score': array([0.92857143, 1. , 1. , 1. , 1. ]), 'mean_test_score': array([0.93333333, 0.93333333, 0.925 , 0.95833333, 0.95833333]), 'std_test_score': array([0.06554109, 0.06497099, 0.06029853, 0.04493161, 0.04493161]), 'rank_test_score': array([3, 3, 5, 1, 1], dtype=int32)}准确度为: 0.9 5.贝叶斯优化算法
上面提到的网格搜索或随机搜索在测试一个新点的时候,会忽略前一个点的信息,而贝叶斯优化则充分利用之前的点的信息。贝叶斯优化算法通过对目标函数形状进行学习,找到使目标函数向全局最优解提升的参数。
主要思想
给定优化的目标函数,通过不断添加样本点来更新目标函数的后验分布,从而调整当前的参数。
通俗点:对目标函数形状进行学习,找到使目标函数向全局最大提升的参数。
具体学习目标函数的方法:
(1)首先根据先验分布,假设一个搜索函数;
(2)每一次使用新的采样点来测试目标函数,利用这个信息更新目标函数的先验分布;
(3)算法测试有后验分布给出全局最优解最可能出现的位置点。
PS先验分布、后验分布、似然估计
参照博客https://blog.csdn.net/qq_40597317/article/details/82388164 了解下什么是先验分布、后验分布、似然估计。
- 先验分布
对未知参数x的先验信息用一个分布形式p(x)来表示。可以理解为对某个原因的经验推断。
举例1:
测量自己的体重,在测量之前就知道自己体重不会超过120斤,不会低于90斤,这个推断可以理解为生活经验所得。
举例2:
老王会走路、骑自行车、或开车去某个地方。假设大家都知道老王是一个健身达人。
那么老王开车去的可能性就比较小,跑步去的可能性就比较大,这个就可以理解为常识得到的先验分布。
- 后验分布
知道事情的结果,然后根据结果推测原因,即该结果由某个原因出现的概率为后验概率。
举例:
还是刚才的老王要去10公里外的地方办事,他可以走路、骑自行车、或者开车,并且花了一定时间才到了目的地。
在这个事件中可以把走路、骑自行车、或开车作为原因,花了一定时间作为结果。
老王花了1小时完成了10公里,则很可能是骑自行车过去,很小可能性跑步,或者开车堵车。
老王花了2小时完成了10公里,则很有可能是走路
花了20分钟,很有可能是开车
先知道结果,然后根据结果估计原因,则称为后验分布。
- 似然估计
与后验分布相反,根据原因推断该原因导致结果发生的概率。
举例:
还是刚才老王,决定步行过去,很有可能10公里需要2个小时;
较小可能性跑步1小时过去;
更有可能骑自行车1小时过去
先确定原因,根据原因来估计结果的概率分布。
两个过程
(1)高斯过程:用以拟合优化目标函数建模,得到其后验分布;
(2)贝叶斯优化:尝试抽样进行样本计算,在局部最优解上不断采样。
贝叶斯优化又分为探索(exploration)和利用(exploitation)两个过程,即进行高效采样。
- 探索就是在还未取样区域去获取采样点;探索意味着方差高
- 开发就是根据后验分布在最可能出现全局最优解的区域去进行采样;开发意味着均值高
贝叶斯优化一旦找到局部最优解,就会在该区域不断采样,容易陷入局部最优解。所以为了弥补这个缺陷,贝叶斯优化算法会在探索(exploration)和利用(exploitation)之间找一个平衡点,基于数据使用贝叶斯定理估计目标的后验分布,然后根据分布选择下一个采样的超参数组合。
与网格搜索、随机搜索区别
(1)贝叶斯优化采用高斯过程,考虑之前的参数,不断更新先验分布;而网格搜索或随机搜索并没有考虑;
(2)贝叶斯优化迭代次数少,速度快;而网格搜索或随机搜索速度慢,参数过多时,容易导致维度爆炸;
(3)贝叶斯优化针对非凸问题依然稳健;而网格搜索或随机搜索对非凸问题得到局部最优
贝叶斯优化缺点在于高斯过程核矩阵不好选
可以做贝叶斯优化的API
BayesianOptimizationbayesoptskopthyperopt...
实例
后面在进行补充对应的实例,因为看到网上的例子都是以随机森林的实例,所以我想先了解下随机森林再来看
总结
对于贝叶斯优化的实例后面会进行补充。加油吧
转载地址:https://blog.csdn.net/nihaomabmt/article/details/103121065 如侵犯您的版权,请留言回复原文章的地址,我们会给您删除此文章,给您带来不便请您谅解!
发表评论
最新留言
关于作者
