本文共 7630 字，大约阅读时间需要 25 分钟。

目录

---

回归

回归：如果目标值为连续性的数据则为回归问题。通常应用场景如下：

房价预测

销售额预测

贷款额度预测

线性回归

定义

线性回归（Linear Regression）是利用回归方程（函数）对一个或多个自变量（特征值）和因变量（目标值）之间的关系建模的一种分析方法。

简答的来说，就是找到一个特定的函数关系，来表示特征值和目标值之间的关系。这个函数关系就是线性模型。通用公式为：

其中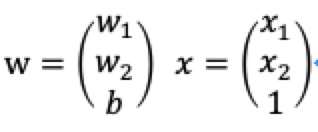

如果只有一个特征则称为单变量回归；如果有多个特征值则称为多变量回归。举个例子：假设房子价格的影响因素可以用下面的一个函数关系表示：

房子价格=0.02x中心区域的距离+0.04x城市一氧化氮浓度+（-0.12x自助房平均价房价）+0.254x城市犯罪率

那我们就可以把这个函数关系称为线性模型。

广义的线性模型

另外还有一种广义的线性模型，虽然是一种非线性关系，但也被称为线性模型。

线性回归中的模型主要分两种：一种是线性关系；另外一种是非线性关系。

线性模型之线性关系

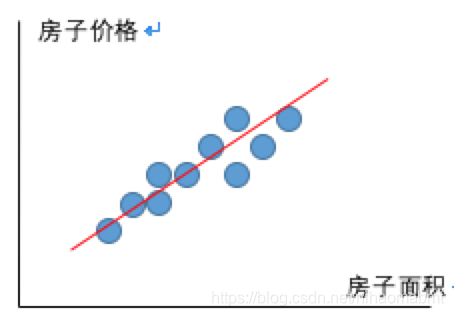
我们在展示房子面积和房子价格之间的时候，可以通过一个线性模型来拟合这条线，此时的这个线就是线性模型，这个关系也是线性关系

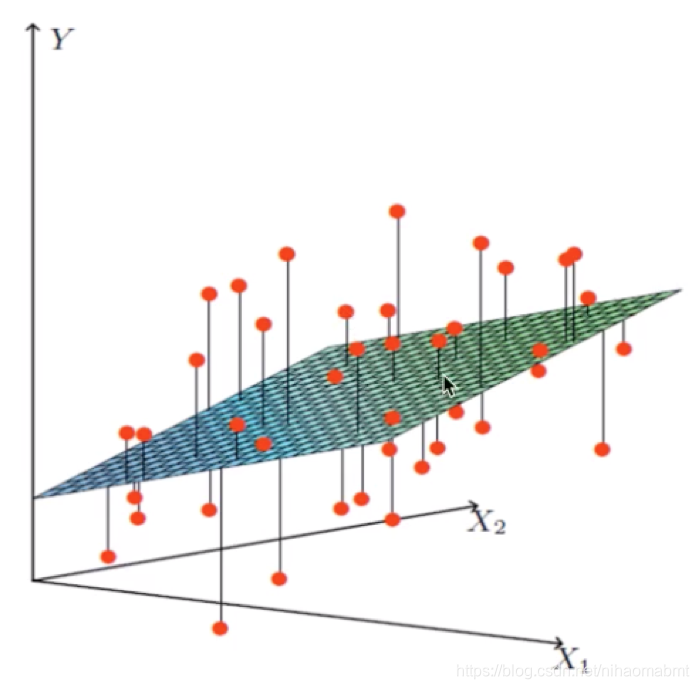
当我们有两个特征值的时候，可以通过一个平面来拟合特征值与目标值之间的关系的时候，此时的线性模型还是线性关系

 

线性模型之非线性关系

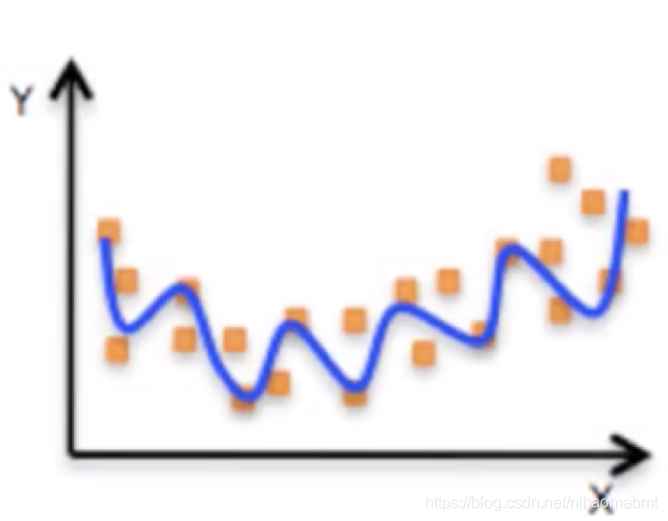
像下面的这个图中，特征值x和目标值y不在简单的是用一条直线来拟合，而是弯曲的，显然x和y不在是线性关系，但是该模型仍然为线性模型。

那么我们对于线性模型可以理解为只要符合下面的任一一种情况之一都属于线性模型：

（1）自变量一次x1,x2...

可以看到特征值和目标值是呈线性关系

（2）参数一次w1,w2...

此时特征值和目标值并不是线性关系，但是参数还是一次，此时该模型仍为线性模型。

综上，线性关系必须是自变量一次，线性关系一定是线性模型，但线性模型并不一定是线性关系。

线性回归模型的求解

线性回归中假定特征值和目标值之间呈线性关系，那么如果得到这个线性模型呢？

目标：只要求出线性模型中的参数，即可以求解出该线性模型，从而使用线性模型进行预测。那我们的目标就是求解出权重和偏置，即回归系数或回归参数。

求解思路：

假设房子的价格和影响房子的价格因素真实存在下面的关系：

真实的房子价格=0.02x中心区域的距离+0.04x城市一氧化碳+（-0.12）x自主房子平均房价

我们可以随意假设所有因素的参数，随便设置各个因素的系数为：

预测房子价格=0.25x中心区域的距离+0.14x城市一氧化碳+0.42x自主房子平均房价。

我们可以看到这些因素对应的参数与真实值之间存在误差，如果我们通过一种方法使得该误差不断缩小，使得误差接近0的时候，那么这个模型的参数就是我们所求的参数。

衡量真实值和预测值之间存在的误差就是损失函数/cost/成本函数/目标函数。这个损失函数所有真实值与预测值之间的距离差的平方之和。在求解这个线性模型的时候，就是去计算出损失函数的最小值，找到误差最小的时候。

损失函数

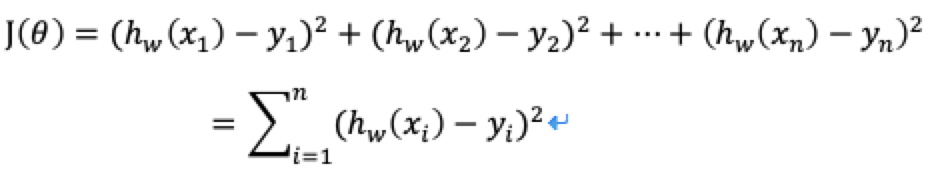
其中y1,y2...为样本的真实值，h(x)为通过预测函数得到的预测值。

有了损失函数，我们在求解这个线性模型的时候，就是去减少损失，然后去求解这个损失函数的最小值，然后该最小值对应的w就是我们所要求解的线性模型的回归系数。

在求解这个损失函数的最小值的时候有两种优化方式：

• （1）正规方程
• （2）梯度下降

下面就分别去介绍下这两种方法：

正规方程

PS几个数学知识：

（1）最小值

我们在求解一个函数的最小值的时候，可以通过先求解函数的导数，然后令导数为0的时候，求解出来的值即找到对应的函数的最小值。假设我们有一个方程式然后去求解最小值：

• 对方程进行求导

• 令导数为0，得到当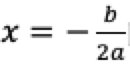的时候，代入到原方程式中，就可以求出y的最小值。

（2）矩阵求逆

如果两个矩阵AxB=E，其中E为单位矩阵，那么

求解过程

有了上面的几个数学知识，我们再来看所谓的正规方程，也称为最小二乘法，就是用方程求解的方式来求解损失函数的最小值，也就是对损失函数求导，然后得到最小值。我们上面的那个公式可以变形为矩阵的形式：

那么对上述的这个公式进行求导，然后令导数为0:

求解出w的过程如下：

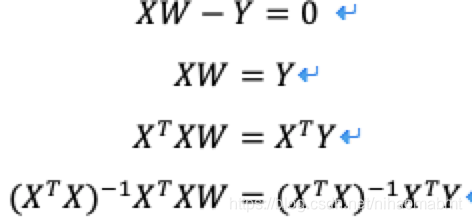
最后得到：

其中X为特征值的矩阵，y为目标值的矩阵，那么我们把样本的特征值和目标值代入到上述的公式中，就可以求解出w的值。

优点：直接通过特征方程进行求解出最好的结果

缺点：当特征过多复杂时，求解速度太慢并且有可能得不到最后的结果

使用场景：数据量比较少的情况下

梯度下降

PS数学小知识

梯度：是一个向量，表示一个函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处  沿着该方向（梯度的方向）变化最快，变化率最大（梯度的模）。

在单变量的函数中，梯度就是函数的导数，代表函数在某个给定点的切线的斜率；

在多变量的函数中，梯度是一个向量。向量有方向，梯度的方向指出了函数在给定点上升最快的方向；而梯度下降就是函数在给定点下降最快的方向，沿着梯度的反方向一直都到局部最低点。

求解过程

Gradient Descent。就是梯度中所有的偏导数都下降到最低点的过程。简单的思路来说：一开始先随便给定一组的w和b，然后不断试错，不断改进，最后得到J(θ)的最小值。也就是沿着切线的方向一点点的下降。

由于在选择初始点是随机的，所以很有可能出现如果函数的图像是一个波浪形，很有可能得到的最低点并不是所有最低点的最小值，但是多次随机就可以解决该问题。

我们刚才提到的损失函数可以用如下的抛物线进行表示：

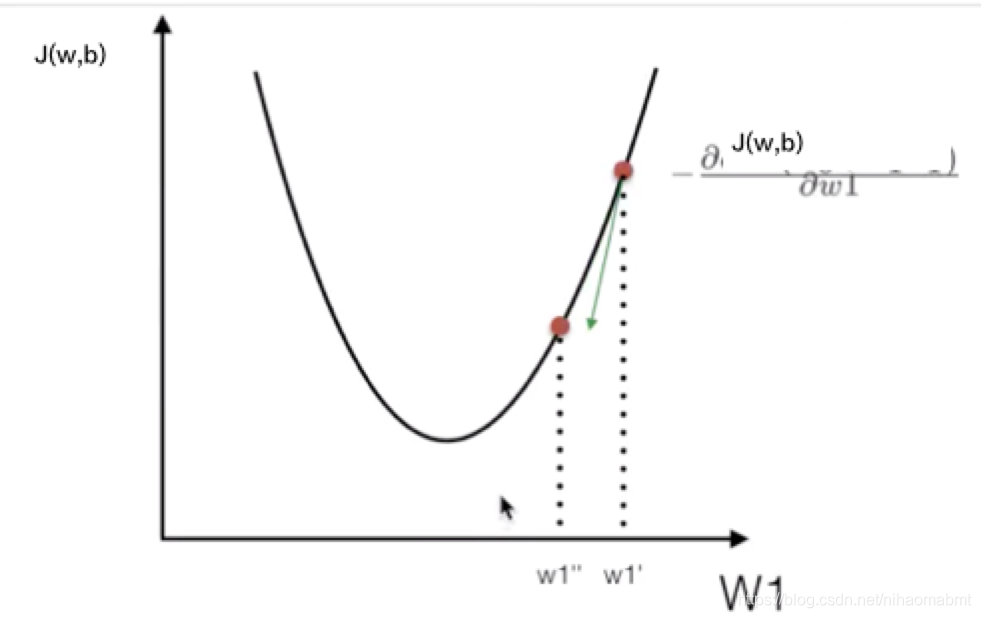
对应的梯度下降的公式也有各种版本，我觉得以我的理解下面的公式能更好的理解梯度下降的概念：

（1）梯度下降对应的求解w和b的公式，初始的时候，先随便给定一个非0的w和b，代入到下面的公式中

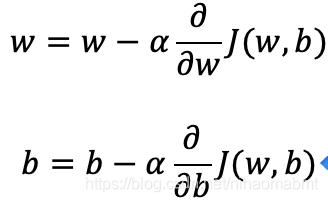
其中为学习率，即沿着坡度每次下降的步长，在调用API的时候需要手动设置，属于超参数。该值不能太大，也不能太小，可以尝试一些值如0.1,0.03,0.01,0.003,0.001,0.0003,0.0001…大了就调小点，小了就调大点；

为坡度下降的方向

2）求解出来的w和b，再一次代入的公式进行求解。直到迭代到达某个数，或者上一次的w和b的值和这一次的结果误差小于某个数的时候，就认为是最优解了。

优点：对于数据集比较大的情况下，可以减少计算复杂度

缺点：如果对于非凸函数，很有可能陷入局部最小值，得到的并不是全局最优解

步长选择过小使得函数收敛速度慢，变大又容易找不到最优解

适用场景：训练数据集十分庞大的时候，能够找到更好的结果。

区分两个概念

凸函数：随便选一个点，梯度下降都可以走到最低点

非凸函数：有很多局部最小值，梯度下降有可能会陷入到局部最小值

梯度下降分类

• 批量梯度下降（BGD）

Batch Gradient Descent

针对整个数据集，对所有样本计算取一个平均值作为每一次梯度下降的步长。这样可以提高准确度，但是需要计算一个维度上的所有数据的梯度，计算复杂度变大。

优点：全局最优解，利于并行

缺点：当样本数据量过大的时候，计算速度慢

• 小批量梯度下降（MBGD）

mini-batch Gradient Descent

将数据分为若干批，分批来更新参数。一组数据共同决定每次梯度下降的步长。

优点：减少计算的开销，降低随机性

• 随机梯度下降（SGD）

每次只随机取一个维度上的一条数据来求梯度，该值作为这个梯度维度下降的步长

优点：计算速度快

缺点：收敛性能不好

          需要许多超参数，比如正则参数、迭代次数

         对于特征标准化是敏感的

• GD

Gradient Descent，原始的梯度下降算法。需要计算所有的样本值才能够计算出梯度

• SAG

随机平均梯度Stochasitc Average Gradient，收敛速度太慢，岭回归和逻辑回归都有SAG的优化

• 区别

批量梯度下降（BGD）：综合所有数据求出梯度，下降的过程一直是很平滑的

随机梯度下降（SGD）：随机抽取一条数据作为参数，步长不稳定

随机梯度下降会比批量梯度下降误差大，但随着迭代次数的增加，误差会越来越小。而随机梯度下降可以看成小批量梯度下降的一个特例。

sklearn中对应的API

上面我们已经讲了可以通过正规方程和梯度下降来求解损失函数的最小值，在sklearn中也提供了对应的API。

• (1)正规方程

sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True,                 n_jobs=None)

其中参数如下：

参数	含义
fit_intercept	是否去计算偏置，默认为true
normalize	是否进行归一化，默认为 False
copy_X	是否复写X，默认为True：X会被复制 False：则X会被复写
n_jobs	可并行的任务数量，默认为1

其返回的参数中：

参数	含义
coef_	回归系数，即线性模型中的w
intercept_	偏置，即线性模型中的b

• （2）随机梯度下降

sklearn.linear_model.SGDRegressor(loss="squared_loss", penalty="l2", alpha=0.0001,                 l1_ratio=0.15, fit_intercept=True, max_iter=1000, tol=1e-3,                 shuffle=True, verbose=0, epsilon=DEFAULT_EPSILON,                 random_state=None, learning_rate="invscaling", eta0=0.01,                 power_t=0.25, early_stopping=False, validation_fraction=0.1,                 n_iter_no_change=5, warm_start=False, average=False)

支持不同的loss函数和正则化惩罚项来拟合线性回归模型。 

其中参数如下：

参数	含义
loss	损失类型。默认为"squared_loss"：普通最小二乘法 'huber'：改进的普通最小二乘法，修正异常值 'epsilon_insensitive'：忽略小于epslion的错误 'squared_epsilon_insensitive'
penalty	惩罚项。默认为l2。 none： l1： elasticnet：
alpha	用来控制对模型正则化的程度，默认为0.0001
l1_ratio	通过该参数来调节岭回归与索套回归的混合比例
fit_intercept	是否计算偏置。默认为True
max_iter	迭代次数
tol	判断迭代收敛与否的阀值
shuffle
verbose
epsilon
random_state	随机种子
learning_rate	学习率的填充。默认为invscaling。即eta=eta0/pow(t,power_t)
eta0	默认0.01
power_t	默认值为0.25
early_stopping
validation_fraction
n_iter_no_change
warm_start
average

其返回的参数中：

参数	含义
coef_	回归系数，即线性模型中的w
intercept_	偏置，即线性模型中的b
n_iter_	实际迭代的次数

线性回归实例

直接使用sklearn中自带的预测波士顿房价的数据集来进行看下上面的两个API的使用。

波士顿房价的数据集的内容如下：

共有13个特征值，506个样本集，其中特征值描述依次为：城镇人均犯罪率、占地面积超过2.5万平方英尺的住宅用地比例、城镇非零售业务地区的比例、查尔斯河虚拟变量 (1 如果土地在河边；否则是0)、一氧化氮浓度（每1000万份）、平均每居民房数、在1940年之前建成的所有者占用单位的比例、与五个波士顿就业中心的加权距离、辐射状公路的可达性指数、每10,000美元的全额物业税率、城镇师生比例、1000（Bk - 0.63）^ 2其中Bk是城镇黑人的比例、人口中地位较低人群的百分数

1.正规方程

from sklearn.linear_model import LinearRegressionfrom sklearn.linear_model import SGDRegressorfrom sklearn.datasets import load_bostonfrom sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScalerfrom sklearn.metrics import  mean_squared_errordef linear():    #1)获取数据集    boston = load_boston()    #2）划分数据集    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)    #3)进行标准化    transfer = StandardScaler()    x_train = transfer.fit_transform(x_train)    x_test = transfer.transform(x_test)    #4)预估器    estimator = LinearRegression()    estimator.fit(x_train, y_train)    #5）进行预测    y_predict = estimator.predict(x_test)    print("线性模型的参数为 w ：", estimator.coef_)    print("线性模型的参数为 b:", estimator.intercept_)    return

我们看下运行结果如下：

线性模型的参数为 w ： [-0.64817766  1.14673408 -0.05949444  0.74216553 -1.95515269  2.70902585 -0.07737374 -3.29889391  2.50267196 -1.85679269 -1.75044624  0.87341624 -3.91336869]线性模型的参数为 b: 22.62137203166228

2.梯度下降

def sgd():    #1)获取数据集    boston = load_boston()    #2）划分数据集    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)    #3)进行标准化    transfer = StandardScaler()    x_train = transfer.fit_transform(x_train)    x_test = transfer.transform(x_test)    #4)预估器    estimator = SGDRegressor(fit_intercept=True, eta0=0.001 )    estimator.fit(x_train, y_train)    #5）进行预测    y_predict = estimator.predict(x_test)    print("线性模型的参数为 w ：", estimator.coef_)    print("线性模型的参数为 b:", estimator.intercept_)    return

运行结果如下：

线性模型的参数为 w ： [-0.40728413  0.70209168 -0.5460648   0.81482482 -1.29062491  3.01039296 -0.22184241 -2.66819966  1.19623538 -0.56932281 -1.64938944  0.90486251 -3.79375431]线性模型的参数为 b: [22.60833855]

回归性能评估

均方误差（Mean Squared Error）MSE用来评估线性回归的效果，其公式如下：

其中yi为预测值，y为真实值。从定义中可以看出和损失函数的差别在于该均方误差除以m。

均方误差越小，则效果越好。

sklearn中的API

mean_squared_error(y_true, y_pred,                       sample_weight=None,                       multioutput='uniform_average'):

其中参数含义如下：

参数	含义
y_true	真实值
y_pred	预测值
sample_weight	样本权重
multioutput	uniform_average：计算所有元素的均方误差，返回的是一个数字 raw_values：返回对应列的均方误差，返回的一个列数相同的数组

对应上述实例的计算

#)模型评估    error = mean_squared_error(y_test, y_predict)

对比两个运行结果的均方误差值为：

正规方程的误差值： 20.627513763095408梯度下降的误差值： 21.670171812236077

在梯度下降使用默认值的情况下，显然正规方程的均方误差要小，但是我们可以通过条件eta0学习率、max_iter迭代次数、learning_rate学习率的算法来减少梯度下降的误差。

总结

梯度下降	正规方程
需要选择学习率	不需要学习率，直接求解
需要迭代求解	一次即可以得出
特征量较大可以使用，适用于大规模数据	需要计算方程，所以适用于小规模的数据，另外岭回归也是适用于小规模数据
	不能解决拟合问题，用的比较少

 

 

转载地址：https://blog.csdn.net/nihaomabmt/article/details/103476956 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！