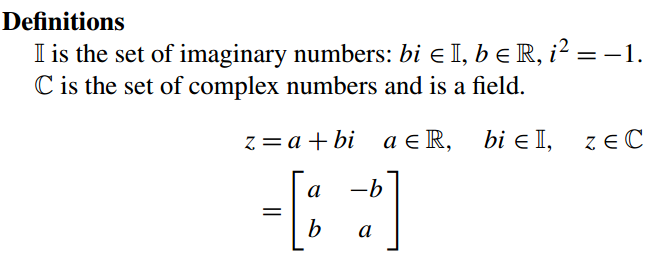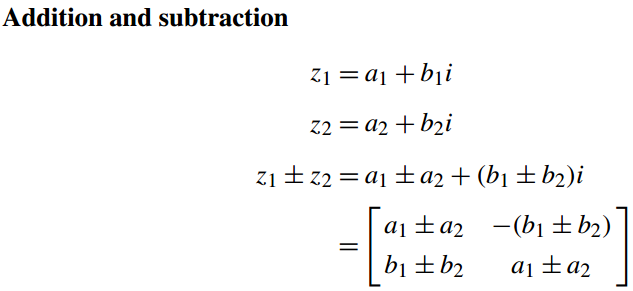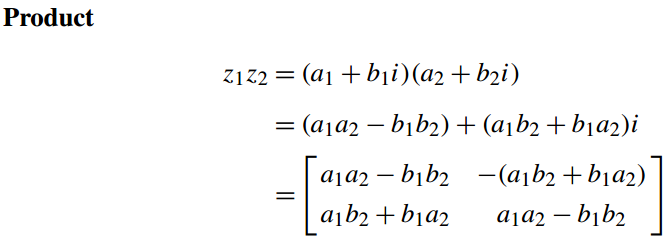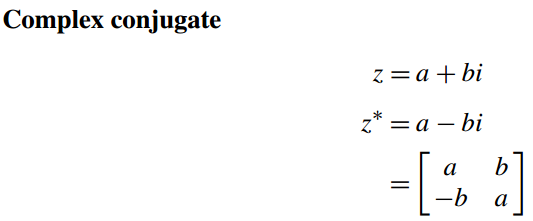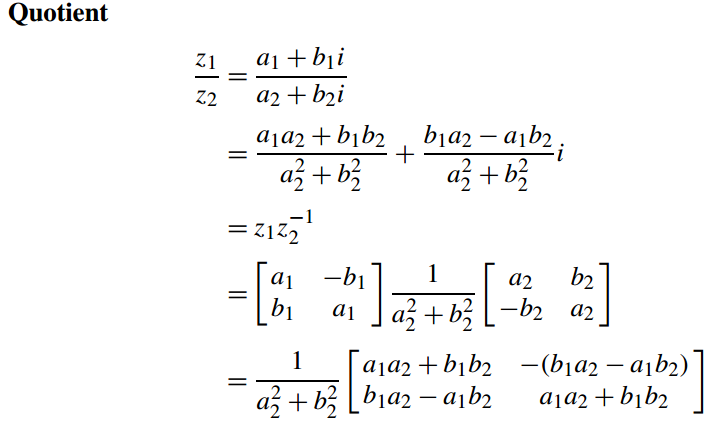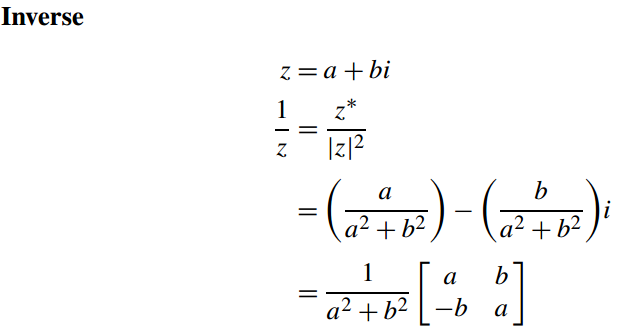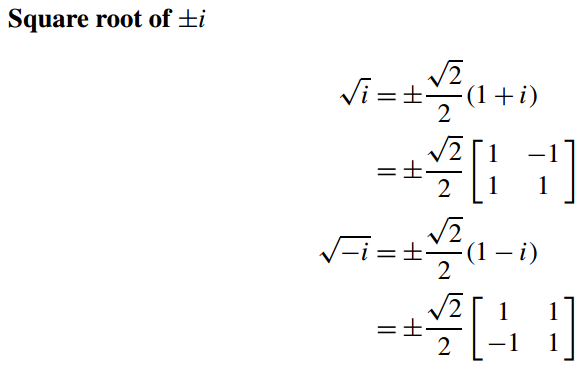本文共 3114 字，大约阅读时间需要 10 分钟。

第三章 复数

 

3.1  介绍

在这一章中我们发现，没有实数根的方程产生方为-1的虚数i。反过来，这把我们引向复数和它们的代数运算。许多与四元数的性质来源于复数，这就是为什么他们是值得仔细研究。

3.2  虚数

虚数是为了解决一个方程没有实数根的问题而发明的，如x2+16＝0。断言数i（i² = -1）存在的简单的想法，允许我们表示这个方程的解为

x =±4i。

它探索i真正是什么是毫无意义的尝试，i真的就是平方为-1的一个东西。然而，它确实有一个图形化的解释，我们将在下一章进行说明。

1637，法国数学家，René Descartes（1596–1650），发表La Géométrie，他在其中表示，将√−1称为“虚”的数字，几个世纪以来都是用这个名词。不幸的是，这是一个贬义词，它没有其他的性质，真的只有平方是−1这一个性质，但当它嵌入代数时会创造一些惊人的结果。

虚数的集合记作I

ib ∈ I, b ∈ R, i² = −1.

3.3  i的幂

当i² = −1，我们还能发现它的其他作用，例如

i⁴ = i²i² = 1andi⁵ = ii⁴ = i.

因此我们有以下结果

i⁰  i¹  i²  i³  i⁴  i⁵  i⁶

1  i  −1  −i  1  i  −1

循环模式（1，i，−1，−i，1，…）是相当惊人的，让我们想起一个类似的模式（x，x，−x，−y，x，…）是由在一个逆时针方向的直角坐标轴旋转所产生。这样的相似性是不能忽略的，因为当实数线与一个垂直的虚轴结合时，就会产生所谓的复平面。但这是后面要讲的。

上述序列概括为：

i⁴ⁿ= 1

i⁴ⁿ⁺¹= i

i⁴ⁿ⁺²= −1

i⁴ⁿ⁺³= −i

其中n ∈ N.

但他的负数幂是什么，我们可以这样考虑i^-1

i⁻¹= 1/i=1(−i)/i(−i)=−i/1= −i.

相似的,

i⁻²= 1/i² =1 /−1= −1

且

i⁻³= i⁻¹i⁻² = −i(−1) = i.

结果如下:

i⁰ i⁻¹  i⁻²  i⁻³  i⁻⁴  i⁻⁵  i⁻⁶

1  −i  −1  i   1  −i   −1

这一次的循环模式是相反的（1，−i，−1，i，1，…）和模式（X，Y−，−X，Y，X，…）类似，这是由平面坐标系按顺时针方向产生。

也许所有幂中最奇怪的是本身：iⁱ，这恰好等于e^{−π/ 2} = 0.207879576…这会在第4章中解释。回顾了虚数i的某些特性后，让我们研究一下当它与实数结合时会发生什么。

3.4  复数

根据定义，一个复数是一个实数和一个虚数的和，表示如下：

z = a +c a ∈ R, c ∈ I.

也可以写为

z = a +bi   a,b ∈ R, i² = −1.

复数的集合用C表示，实数也是复数，只不过没有虚部。也就是说实数和虚数都是复数的子集，表达式为

R ⊂ C

I ⊂ C

虽然一些数学家把i放在乘数前面：i4，一些放在乘数后面：4i，这是本书用放在后面的。然而，当i与三角函数相关时，将它放在函数前面是很好的做法，以避免与三角函数的角度混淆。例如，sinαi可以暗示角是虚的，而isinα则意味着sinα的值是虚数。

通常我们把复数写为a+bi，并赋予它实数的公理，如交换律，分配律等

3.5  复数加减法

有两个复数

z₁ =a₁ + b₁i

z₂= a₂ + b₂i

则

z₁± z₂ = (a₁ ± a₂) + (b₁ ± b₂)i

3.6  复数的数乘

对于复数a+bi，乘以个数字λ为

λ(a + bi) = λa + λbi

3.7  复数相乘

有两个复数

z₁ =a₁ + b₁i

z₂= a₂ + b₂i

theirproduct is

z₁z₂= (a₁ + b₁i)(a₂ + b₂i)

= a₁a₂+ a₁b₂i + b₁a₂i + b₁b₂i²

= (a₁a₂− b₁b₂) + (a₁b₂ + b₁a₂)i

3.7.1  复数的平方

复数z=a+bi的平方为

z² =(a + bi)(a + bi)

= (a2 −b2) + 2abi.

3.8  复数的模

复数z=a+bi的模或绝对值写为|z|，定义是

|z| = √(a² + b²).

3.9  共轭复数

如果只有虚部符号不同的两个复数相乘会得到下面这个特殊的结果

(a +bi)(a − bi) = a² − abi + abi − b2i²= a² + b².

我们把a-bi称为z=a+bi的共轭复数，记作z^*，有如下性质

zz^∗ = a² + b² = |z|².

3.10  两个复数之比

共轭复数为我们提供了复数除法的思路

(a₁+ b₁i)/(a₂ + b₂i)

=(a₁+ b₁i)(a₂ − b₂i)/(a₂ + b₂i)(a₂− b₂i)

=(a₁a₂− a₁b₂i + b₁a₂i − b₁b₂i²)/(a₂²+ b₂²)

=(a₁a₂+ b₁b₂)|z|² +(b₁a₂ − a₁b₂)/|z|²i.

3.11复数的逆

复数z=a+bi为

z^-1=1/z=z^*/(zz^*)=z^*/|z|²=[a/(a²+b²)]-[a/(a²+b²)]i

3.12  i的根

令i由a+bi平方求得，则

i = (a +bi)(a + bi)

= a²+ 2abi − b²

= a²− b² + 2abi

则

a²− b²=0，2ab=1

在此我们令a，b相等，则

a = b =√2/2

因此，√i为

√i = ±√2/2(1 + i)

同理令a = b =√2/2i

得√-i为

√-i = ±√2/2(1 - i)

3.13域结构

复数集合C是一个域，因为他满足域的所有定义。

3.14有序对

复数z=a+bi的实部和虚部为

Re(a +bi) = a

Im(a +bi) = b

把它写为上章中的有序对的形式（a，b），则加法和乘法为

z₁= (a₁, b₁)

z₂= (a₂, b₂)

z₁+ z₂ = (a₁ + a₂,b₁ + b₂)

z₁z₂= (a₁a₂ − b₁b₂,b₁a₂+ a₁b₂).

3.14.1数乘

3.14.2共轭

3.14.3除法

3.14.4求逆

均和复数的一般形式的结果相同，只是用有序对来表示，在此不再赘述。

3.15复数的矩阵表示

作为四元数有一个矩阵表示，也许我们应该研究复数的矩阵表示。我们可以认为复数的矩阵C是表示实数矩阵R和虚数矩阵I之和：

C=R+I=aR’+bI’,

R’可以看做1，在矩阵中为单位矩阵。

虽然我只是前面暗示过i可以看作是某种旋转算子，这里就是显示它的完美的方式。在4章我们会发现一个复数乘以i能有效地转动90°。因此，它可以用90°的旋转矩阵来表示：

[cos90,-sin90;

sin90,cos90]=

[0,-1;

1,0]

所以

C=[a,-b;b,a]=a[1,0;0,1]+b[0,-1;1,0]

3.15.1矩阵形式相加

3.15.2矩阵形式相乘

3.15.3矩阵形式的模

3.15.4矩阵形式的共轭

3.15.5矩阵形式的逆

3.15.6矩阵形式的除法

上述均可根据矩阵的运算法则求出，在此不再赘述

3.16总结

我们在这一章表明复数集是一个域，因为他们满足封闭性，结合律，分配律，单位元，逆元。我们还证明了复数和有序对之间存在一一对应关系，复数可以表示为一个矩阵，它允许我们计算所有复数运算为矩阵运算。

如果这是你第一次遇到复数，一方面你可能会发现它们很奇怪，另一方面也觉得很奇妙。只是简单地宣布−1的根i的存在，就开辟了一个新的数字系统，扩展了数学的领域。

3.16.1操作总结

转载地址：https://blog.csdn.net/yukinoai/article/details/79057511 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！