
本文共 7747 字,大约阅读时间需要 25 分钟。
文章目录
- 为拟合某函数 f f f
- 即定义映射 y = f ( x ; θ ) y=f(x;\theta) y=f(x;θ)
- 将输入 x x x转化为某种预测的输出 y y y
- 并同时学习网络参数 θ \theta θ
- 使模型得到最优函数近似
- 深度前馈网络由多个函数复合在一起表示
- 该模型与ー个有向无环图关联
- “链式结构” f ( x ) = f ( 3 ) ( f ( 2 ) ( f ( 1 ) ( x ) ) ) f(x)=f^{(3)}(f^{(2)}({f^{(1)}(x)})) f(x)=f(3)(f(2)(f(1)(x)))
- 链长为网络模型“深度”
- 设真实函数为 f ∗ ( x ) f^{*}(x) f∗(x),在神经网络过程中
- 试图令 f ( x ) f(x) f(x)拟合 f ∗ ( x ) f^*(x) f∗(x),
- 训练数据则提供在不同训练点上取值的 f ∗ ( x ) f^*(x) f∗(x)的近似实例(可能含噪声)
- 即每样本 x x x伴随一个标签 y ≈ f ∗ ( x ) y\approx f^*(x) y≈f∗(x),
- 指明输出层必须产生接近标签的值
- 网络学习算法则需決定如何用中间的“隐藏层”来实现最优近似
- 深度前馈网络是一类网络模型
- 多层感知机、自编码器、限制玻尔兹曼机,
- 及卷积神经网络
1 多层感知机与布尔函数
场景描述
- 大脑皮层的感知与计算功能是分层实现
- 光信号进入大脑皮层V1区,
- 初级视皮层,
- 之后通过V2层和V4层,即纹外皮层,
- 进入下颞叶参与物体识别
- 深度神经网络除模拟人脑功能的多层结构
- 最大优势在于能以紧凑、简洁的方式
- 来表达比浅层网络更复杂的函数集合
- (简洁”:隐层单元数目与输入单元数目呈多项式)
- 最大优势在于能以紧凑、简洁的方式
- 每节点都可与/或/非
- 咋构造一个MLP实现
- n n n输入比特的奇偶校验码(任意布尔函数)?
多层感知机表示异或时最少要几个隐层(二元输入)?
- 零个隐层(等同于逻辑回归)能否表示异或。

- 逻辑回归公式 Z = s i g m o i d ( A X + B Y + C ) (9.1) Z=sigmoid(AX+BY+C)\tag{9.1} Z=sigmoid(AX+BY+C)(9.1)
- Sigmoid单増
- Y=0时,
- 将X从0变到1将使输出Z也从0变为1
- 说明需设A为正
- 逻辑回归(不带隐层的感知机)无法精确学习出异或
- 通用近似定理:
- 一个前馈神经网络
- 如果有线性输出层和
- 至少一层具有任何一种“挤压”性质的激活函数的隐藏层
- 当给予网络足够数量的隐藏单元时
- 可任意精度近似任何
- 从一个有限维空间到另一个有限维空间的波菜尔可测函数
- 常用的激活函数和目标函数是
- 通用近似定理适用的一个子集,
- 因此MLP的表达能力强
- 关键是否能学习到对应此表达的参数

- 这里设计参数以说明含一个隐含层的多层感知机就可异或,图9.1
- 等同于计算 H 1 = X + Y − 1 H_1=X+Y-1 H1=X+Y−1,再用ReLU,如表9.2。
- 第一个隐藏单元在X和Y均为1时激活
- 第二个隐藏单元在X和Y均为0时激活,
- 最后将两个隐藏单元的输出
- 做线性变换即可,表9.4

如果只一个隐层,需多少隐节点能实现含n元输入的任意布尔函数?
- n元输入的任意布尔函数可唯一表示为析取范式
- (Disjunctive Normal Form)
- (由有限个简单合取式构成的析取式)

- 由如图9.2表示

3多层感知机的反向传播算法
场景描述
- l l l层的输入 x ( l ) x^{(l)} x(l),输出为 a ( l ) a^{(l)} a(l)
- 每一层先用输入 x ( l ) x^{(l)} x(l)和偏置 b ( l ) b^{(l)} b(l)计算仿射变换
z ( l ) = W ( l ) x ( l ) + b ( l ) z^{(l)}=W^{(l)}x^{(l)}+b^{(l)} z(l)=W(l)x(l)+b(l)
-
然后激活函数 f f f作用 z ( l ) z^{(l)} z(l),得 a ( l ) = L W , b ( x ( l ) ) = f ( z ( l ) ) a^{(l)}=\mathcal{L}_{W,b}(x^{(l)})=f(z^{(l)}) a(l)=LW,b(x(l))=f(z(l))
-
a ( l ) a^{(l)} a(l)直接作为下一层的输入,即 x ( l + 1 ) x^{(l+1)} x(l+1)
-
x ( l ) x^{(l)} x(l): m m m维
-
z ( l ) z^{(l)} z(l)和 a ( l ) a^{(l)} a(l)为n维
- W ( l ) W^{(l)} W(l)为 m × n m\times n m×n维矩阵
上面明显有错误!
- z i ( l ) z_i^{(l)} zi(l), a i ( l ) a_i^{(l)} ai(l), W i j ( l ) W_{ij}^{(l)} Wij(l)表其中元素

第 l − 1 l-1 l−1层有 m l − 1 m_{l-1} ml−1个神经元!
- 网络训练中,前向传播产生一个标量损失函数
- BP则将损失函数的信息沿网络层向后传播用以计算梯度
- 达到优化网络参数
- 反向传播是神经网络中非常重要,
- 从业者需要对反向传播算法熟悉掌握并灵活应用
多层感知机的平方误差和交叉熵损失函数
- 样本集合 { ( x ( m ) , y ( m ) ) } \{(x^{(m)},y^{(m)})\} { (x(m),y(m))}

- 第一项平方误差项,
- 第二项为L2正则化项,
- 功能上可称作权重衰减项,
- 减小权重的幅度,防止过拟合。
- λ λ λ为权重衰减参数,
- 控制损失函数中两项的相对权重
- 二分类场景为例,交叉熵损失函数

- 正则项与上式是相同
- 第一项衡量了预测 o ( i ) o^{(i)} o(i)与真实类別 y ( i ) y^{(i)} y(i)之间的交叉熵
- 当 y ( i ) y^{(i)} y(i)与 o ( i ) o^{(i)} o(i)相等时,熵最大,损失函数最小
- 多分类场景中,类似地写出相应的损失函数
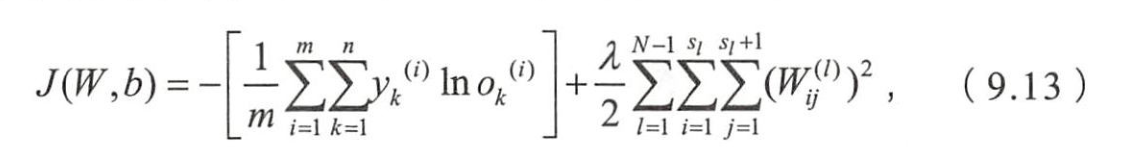
- o k ( i ) o_k^{(i)} ok(i)代表第 i i i样本的预测属于类别 k k k的概率
- y k ( i ) y_k^{(i)} yk(i)为实际的概率
- 第 i i i个样本的真实类别为 k k k,则 y k ( i ) = 1 y_k^{(i)}=1 yk(i)=1,否则0
2 问题1中定义的损失函数,推导各层参数更新的梯度
- 第 ( l ) (l) (l)层的参数为 W ( l ) W^{(l)} W(l)和 b ( l ) b^{(l)} b(l)
- 每一层的线性变换为 z ( l ) = W ( l ) x ( l ) + b ( l ) z^{(l)}=W^{(l)}x^{(l)}+b^{(l)} z(l)=W(l)x(l)+b(l)
- 输出为 a ( l ) = f ( z ( l ) ) a^{(l)}=f(z^{(l)}) a(l)=f(z(l))
- f为Sigmoid、Tanh、ReLU等)
- a ( l ) a^{(l)} a(l)直接作为下ー层的输入
- x ( l + 1 ) = a ( l ) x^{(l+1)}=a^{(l)} x(l+1)=a(l)
- 可用批量梯度下降法来优化网络参数。
- 梯度下降法中每次迭代对参数W(网络连接权重)和b(偏置)更新

- α \alpha α控制每次迭代中梯度变化幅度。
- 问题的核心为求解那两个
- 为得到递推公式
- 还需计算损失函数对隐含层的偏导
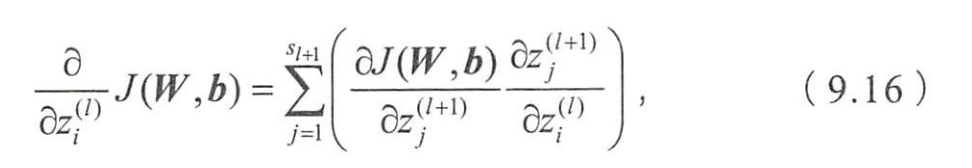
- z i ( l ) z_i^{(l)} zi(l)不就是第 l l l层第 i i i个节点的加权和马
- 已经包含偏置啦哈哈哈
- S l + 1 S_{l+1} Sl+1为 l + 1 l+1 l+1层的节点数
- 而
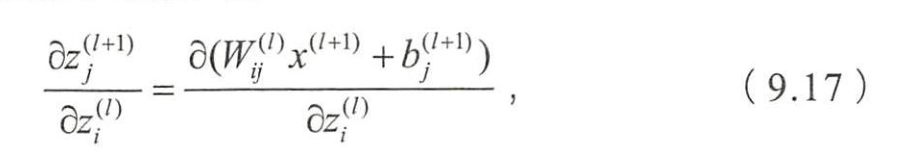
上面应该是
∂ z j ( l + 1 ) ∂ z i ( l ) = ∂ ( W i j ( l + 1 ) x i ( l + 1 ) + b j ( l + 1 ) ) ∂ z i ( l ) (9.17) \frac{\partial{z_j^{(l+1)}}}{\partial{z_i^{(l)}}}=\tag{9.17}\frac{\partial{(W_{ij}^{(l+1)}x_i^{(l+1)}+b_j^{(l+1)})}}{\partial{z_i^{(l)}}} ∂zi(l)∂zj(l+1)=∂zi(l)∂(Wij(l+1)xi(l+1)+bj(l+1))(9.17)
- 9.17可写为
x i ( l + 1 ) = a i ( l + 1 ) = f ( z i ( l ) ) x_i^{(l+1)}=a_i^{(l+1)}=f(z_i^{(l)}) xi(l+1)=ai(l+1)=f(zi(l))


- 看作损失函数在第 l l l层第 i i i个节点产生的残差量
- 记为 δ i ( l ) \delta_i^{(l)} δi(l),
这样的即使我很开心!解释地太好了!注意这里的 z i l z_i^{l} zil是第 l l l层的第 i i i个神经元的未激活之前的值!
- 递推公式

δ i ( l ) = ∑ j = 1 s l + 1 ( W i j ( l ) δ j ( l + 1 ) ) f ′ ( z i ( l ) ) (9.19) \delta_i^{(l)}=\sum_{j=1}^{s_{l+1}}\left(W_{ij}^{(l)}\delta_j^{(l+1)}\right)f'(z_i^{(l)})\tag{9.19} δi(l)=j=1∑sl+1(Wij(l)δj(l+1))f′(zi(l))(9.19)
- 损失对参数函数梯度可写为

我严重怀疑:9.21的左边两坨是接在9.20上面的
我严重怀疑:9.21的右边应该写错了!应该是 ∂ ∂ b i ( l ) J = δ i ( l ) \frac{\partial{}}{\partial{b_i^{(l)}}} J=\delta_i^{(l)} ∂bi(l)∂J=δi(l)
- 下针对两种不同的损失函数计算最后一层的残差 δ ( L ) \delta^{(L)} δ(L)
- 其他层的残差 δ ( L − 1 ) , . . . , δ ( 1 ) \delta^{(L-1)},...,\delta^{(1)} δ(L−1),...,δ(1)可根据上面得到的递推公式计算。
为啥不说出来是第几层的哪个神经元呢?
- 为简化起见,忽略Batch样本集合和正则化项的影响,
- 重点关注这两种损失函数产生的梯度。

注意:上面的 y y y是个向量!同样 z ( L ) z^{(L)} z(L)也是向量!

4神经网络训练技巧
- 大规模神经网络的训练过程中,常常面临“过拟合”的问题,即当参数 数目过于庞大而相应的训练数据短缺时,模型在训练集上损失值很小,但在测试集上损失较大,泛化能力很差。
- 解決“过拟合”的方法有很多,
- Data Augmentation、
- 参数范数惩罚/正则化( Regularization)、
- 模型集成(Mode Ensemble)等;
- Dropout是模型集成方法中最高效与常用的技巧。
- 深度神经网络的训练中涉及诸多手调参数,
- 如学习率、权重衰减系数、 Dropout比例等,这些参数的选择会显著影响模型最终的训练效果。
- 批量归一化( Batch Normalization,BN)有效规避了这些复杂参数对网络训练产生的影响,加速训练收敛也提升了网络的泛化能力。
神经网络训练时是否可以将全部参数初始化为0?
- 考虑全连接的深度神经网络,同一层中的任意神经元都是同构的 它们拥有相同的输入和输出,如果再将参数全部初始化为同样的值,那 么无论前向传播还是反向传播的取值都是完全相同的。
- 学习过程将永远无法打破这种对称性,最终同一网络层中的各个参数仍然是相同的
- 因此,要随机地初始化神经网络参数的值,以打破这种对称性。
- 可初始化参数为取值范围 ( − 1 d , 1 d ) (-\frac{1}{\sqrt{d}},\frac{1}{\sqrt{d}}) (−d1,d1)的均匀分布,
- d是一个神经元接受的输入维度。
- 偏置可以被简单地设为0,并不会导致参数对称的问题。
我觉得他说的非常对,如果都是初始化成零的话,每个结点的确是同质的!那么他们这个对称的就无法打破这个对衬性,我觉得这个说的非常正确。
为什么 Dropout可以抑制过拟合?它的工作原理和实现?
- 以一定概率随机“临时丢弃”一部分神经元节点。
这个临时的词用得好!
- Dropout作用于每份小批量训练数据
- 其随机丢弃部分神经元的机制
- 相当于每次迭代都在训练不同结构的神经网络
- 类比于Bagging,
- Dropout可被认为是种实用的大规模深度神经网络的模型集成算法
- 传统意义上的Bagging涉及多个模型的同时训练与测试评估,
- 当网络与参数规模庞大时,
- 这种集成方式需要消耗大量的运算时间与空间。
- Dropout在小批量级别上的操作,
- 提供一种轻量级Bagging集成近似,
- 能实现指数级数量神经网络的训练与评测測
- 要求某个神经元节点激活值以概率P被“丢弃”,
- 即该神经元暂时停止工作,图9.12
- 对包含 N N N个神经元节点的网络,在 DropoutF的作用下可看作为 2 N 2^N 2N个模型集成。
- 这 2 N 2^N 2N个模型可认为是原始网络的子网络,它们共享部分权值,
- 并有相同网络层数,而模型整体参数数目不变,这就大大简化运算。
- 对任意神经元,
- 每次训练中都与一组随机挑选的不同的神经元集合共同优化,
- 这个过程会减弱全体神经元之间的联合适应性
- 减少过拟合的风险,增强泛化能力。
- 用Dropout包括训练和预测两阶段。
- 训练阶段中,每个神经元节点需増加一个概率系数,如图9.13。
- 训练阶段又分前向传播和反向传播两步骤。
- 原始网络对应的前向传播公式为


- 应用 Dropout之后,前向传播公式变为

5 深度CNN
场景描述
- CNN特点
- 每层神经元节点只响应前一层局部区域范围内的神经元
- (全连接网络中每个神经元节点响应前一层的全部)
- DCNN
- 通常由若干巻积层叠加若干全连接层组成,
- 中间也包含各种非线性操作及池化操作
- 卷积神经网络同样可用反向传播算法训练,
- 卷积操作的参数共享特性使要优化的参数数目大大缩减,
- 提高模型的训练效率以及可扩展性。
- 卷积运算主要用于处理类网格结构的数据,
- 对于时间序列及图像数据的分析与识别具有优势
- 图9.14是CNN的一个经典结构示意图。
- Lecun Yani在98年提出的卷积神经网络结构
- 输入在经历几次卷积和池化层的重复操作之后
- 接入几个全连通层并输出预测结果,
- 已成功应用于手写体识别

卷积操作的本质:稀疏交互和参数共享,这两种特性及其作用。
6深度残差网络
场景描述
- 数据规模增加,使有可能训练更大容量的模型,不断地提升模型的表示能力和精度
- 深度神经网络的层数决定模型容量,
- 层数的加深,优化函数陷入局部最优
- 随着网络层增加,梯度消失更严重,
- 梯度在反向传播时会逐渐衰减
- 特别是Sigmoid激活函数,使远离输出层(即接近输入层)的网络层不能够得到有效的学习,影响模型泛化
- 过去十几年间尝试了许多方法
- 改进训练算法、正则化、设计特殊的网络结构
- Resnet是有效的网络结构改进,极大提高可以有效训练的深度神经网络层数
- Resnet在 Imagenet和 Alphago Zero的应用中都取得非常好效果
- 15年时,用Resnet训练的模型已达152,且相较往年取得很大提升
- 如今可用深度残差网络训练拥有成百上干层的模型

Resnet的提出背景和核心理论?
- 深层的神经网络训练中的梯度消失
- L层的深度神经网络,在上面加入一层得到的L+1层深度神经网络的效果应该至少不会比L层的差
- 简单地设最后一层为前一层的拷贝(用一个恒等映射即可),且其他层维持原来参数
- 反向传播时,很难找到这种形式解。
- 实验发现,层数更深的神经网络反而会更大训练误差。
- CIFAR-10上的一个结果如图9.22,
- 56层比20层的网络训练误差大
- 很大程度上归结于梯度消失

- 为解释梯度消失问题如何产生
- 3节推导出的误差传播公式

对 z i ( l ) z^{(l)}_i zi(l)就是==!上面写错了!
- 再展开一层

- 误差传播可写成参数 W i j ( l ) W_{ij}^{(l)} Wij(l)、 W j k ( l + 1 ) W_{jk}^{(l+1)} Wjk(l+1)
- 及导数 f ′ ( z j ( l + 1 ) ) f'(z_j^{(l+1)}) f′(zj(l+1))、 f ′ ( z j ( l ) ) f'(z_j^{(l)}) f′(zj(l))连乘
- 当误差由第 L L L层( δ i ( L ) \delta_i^{(L)} δi(L))
- 传到除输入以外第一隐层( δ i ( 1 ) \delta_i^{(1)} δi(1))时,
- 会涉及非常多参数和导数连乘,
- 这时误差很容易消失或膨胀,影响对该层参数正确学习。
- 因此深度神经网络的拟合和泛化能力较差
- 有时甚至不如浅层
- Resnet调整网络结构
- 先考虑两层网络(9.23(a)),输入 x x x经两个网络层的变换得到H(x)
- 反向传播时,梯度涉及两层参数的交叉相乘,
- 可能在离输入近的网络层中产生梯度消失
- Resnet:
- 既然离输入近的神经网络层难训练,那可将它短接到更靠近输出的层,如图(b)
- 输入 x x x经两个神经网络的变换得 F ( x ) F(x) F(x),同时也短接到两层之后,最后这个包含两层的神经网络模块输出 H ( x ) = F ( x ) + x H(x)=F(x)+x H(x)=F(x)+x
- 这样, F ( x ) F(x) F(x)被设计为只需要拟合输入 x x x与目标输出 H ~ ( x ) \tilde{H}(x) H~(x)的残差 H ~ ( x ) − x \tilde{H}(x)-x H~(x)−x
- 如果某一层输出已较好的拟合了期望结果
- 那多加入层不会使得模型变得更差,因为该层的输出将直接被短接到两层之后,相当于直接学习了一个恒等映射,而跳过的两层只需要拟合上层输出和目标之间的残差即可

- Resnet可有效改善深层的神经网络学习问题,使训练更深的网络成可能
- 图9.24(a)展示传统神经网络的结果,
- 随着模型结构的加深训练误差反而上升;
- 而图9.24(b)是Resnet的实验结果,随着模型结构的加深,训练误差逐渐降低,并且优于相同层数的传统的神经网络。

转载地址:https://cyj666.blog.csdn.net/article/details/104841724 如侵犯您的版权,请留言回复原文章的地址,我们会给您删除此文章,给您带来不便请您谅解!
发表评论
最新留言
关于作者
