
本文共 3141 字,大约阅读时间需要 10 分钟。
文章目录
今天要学习的算法是莫队算法基础版本。
1. 莫队概述
莫队是一种解决区间查询问题的离线算法。它的思想很简单,本质上就是通过挪动区间的方式按照某种顺序,离线处理区间查询操作。
它的时间复杂度是 O(n n ) \text{O(n}\sqrt{n}) O(nn) ,是一种效率不错的算法,可以解决几乎所有的区间查询问题(需要离线),只要对时间复杂度的要求不是那么苛刻。
2. 挪动区间
假设有这样的一道题:对于一个数列,每次给出一个区间询问 [L,R] ,求它的区间和。这道题用前缀和很容易做出来,不过我们强制用莫队做。
对于下面的例子,首先要开一个数组存储数列。注意,区间从 1 开始:
0 1 2 3 4 5 6 7 8 9 |index 3 8 1 2 7 4 9 0 6 |val
假设我们此时已经知道 [2,5] 区间的和是 18 ,有如下询问:
- 求
[2,6]区间的和:用[2,5]区间的和,加上第六项的值即可,答案是18+4=22; - 求
[2,4]区间的和:用[2,5]区间的和,减去第五项的值即可,答案为18-7=11; - 求
[3,6]区间的和:用[2,5]区间的和,减去第二项的值,再加上第六项的值就可以求出; - 其他区间依次类推。
由此,对当前区间 [L,R] ,我们分别讨论四种情况:
- 加上当前区间左边一格
L - 1处的贡献:Add(--L); - 加上当前区间右边一格
R + 1处的贡献:Add(++R); - 减去当前区间最左一格
L处的贡献:Sub(L++); - 减去当前区间最右一格
R处的贡献:Sub(R--);
可以看到,我们不只是修改了区间的总贡献,还修改了区间的 [L, R] 边界。这样,所有的区间都可以从当前已知区间的结果扩展出来。
3. 某种顺序和离线处理
仅仅这样是远远不够的,对于一个 n 项的数列,假设这样询问 m 次:
[1,2], [n-1,n], [1,2], [n-1,n] ...
无疑,时间复杂度爆炸了,它将变成一个 O(mn) \text{O(mn)} O(mn) 的算法。但是对于同样的这些询问,如果是以下的顺序:
[1,2], [1,2] ... [n-1,n], [n-1,n] ...
时间复杂度瞬间优化到 O(m+n) \text{O(m+n)} O(m+n) ,速度大大提升。可见,询问顺序对莫队算法的时间复杂度有着很大的影响。甚至可以说,莫队算法要满足的必要条件就是必须以接近 O(1) \text{O(1)} O(1) 的时间移动区间。如果可以在 O ( 1 ) O(1) O(1) 内从 [ l , r ] [l,r] [l,r] 的答案,移动到 [ l − 1 , r ] , [ l + 1 , r ] , [ l , r − 1 ] , [ l , r + 1 ] [l-1,r], [l+1, r], [l, r-1], [l, r+1] [l−1,r],[l+1,r],[l,r−1],[l,r+1] 这四个与之紧邻的区间并得出答案,就可以考虑使用莫队。
那么怎样排序来解决询问顺序呢?很容易想到使用 l l l 作为第一个关键字、 r r r 作为第二关键字进行排序,但这样的效果不是很好。为此,我们需要使用分块进行优化。具体做法如下:
- 首先分块,块大小就是普通的 n \sqrt{n} n ;
- 然后对所有的询问进行排序,排序规则如下:对于一个询问
[L,R],首先按照区间的L边界所在块的编号从小到大排序;对于处在同一块的,按照R的大小进行排序; - 排序后,遍历所有询问,进行区间的移动,得到各个询问的答案记录下来;
- 最后,按照这些询问的原顺序输出答案即可。
看完上面的过程,我们就能够明白,为什么莫队要求离线。
4. 莫队算法框架
下面给出基础莫队的代码框架:
#includeusing namespace std;const int maxn = 5e4 + 5;int a[maxn]; //记录所有数据的数组int pos[maxn]; //a数列中的第几项是第几块的 int ans[maxn]; //记录所有询问的答案(按照原来的顺序)//询问的结构体struct Q { int l, r, k; //询问的区间[l,r], 第几个询问 } q[maxn];//记录某一个由[L,R]规定的闭区间的区间结果int res = 0;//挪动区间的函数void Add(int n) { ... }void Sub(int n) { ... }int main() { //n个数据,m个询问 int n, m; cin >> n >> m; //记录数据和分块 int size = sqrt(n); //块的大小 for (int i = 1; i <= n; ++i) { cin >> a[i]; pos[i] = i / size; //每个数据处于哪一块 } //记录询问 for (int i = 0; i < m; ++i) { cin >> q[i].l >> q[i].r; q[i].k = i; //第几个询问,用来记录询问的原始顺序 } //所有询问进行排序,同一个块按照r排序,否则按照块顺序排 sort(q, q + m, [](Q x, Q y) { return pos[x.l] == pos[y.l] ? x.r < y.r : pos[x.l] < pos[y.l] }); //当前所知的闭区间[l,r] int l = 1, r = 0; //遍历所有的询问 for (int i = 0; i < m; ++i) { while (q[i].l < l) Add(--l); while (q[i].r > r) Add(++r); while (q[i].l > l) Sub(l++); while (q[i].r < r) Sub(r--); //按照原始顺序记录答案 ans[q[i].k] = res; } //输出ans数组作为答案 ... return 0;}
5. 应用题
基础莫队:
基础莫队: 基础莫队:6. 常数优化:奇偶化排序
上面的分块排序,就可以有效降低每两次询问间 l , r l, r l,r 移动的距离。但在此之上,我们还可以进行常数优化:奇偶化排序。即块号 pos[l] 不相等时,按照块号从小到大排序;相等时如果 pos[l] 是奇数,则将 r 从小到大排序,否则按照 r 从大到小排序。为什么它是有效的?
如果按照一般的排序方法,指针会这样移动:在 l 处于同一块时,指针 r 不断往右移;每当 l 跨越一个块时,r 都必须从右向左移动很长一段距离:
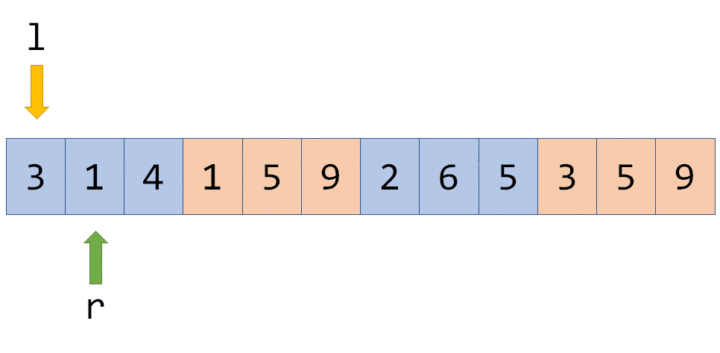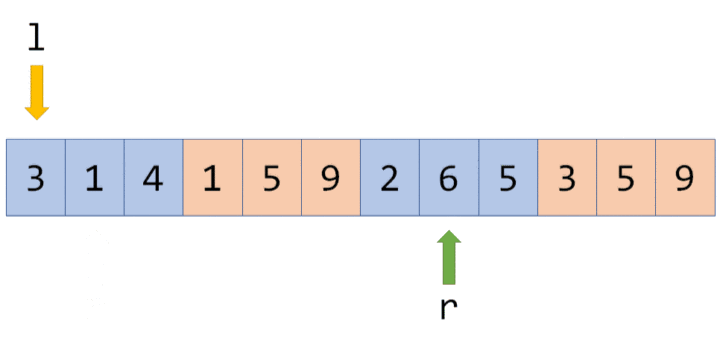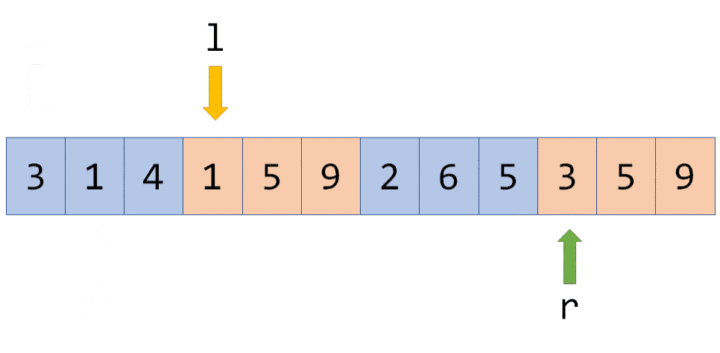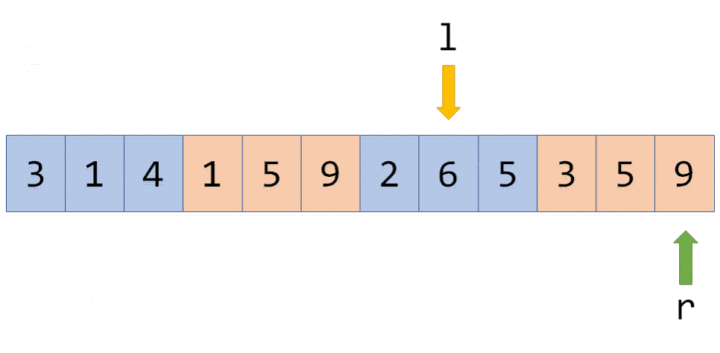 而奇偶化排序后,指针会这样移动:在
而奇偶化排序后,指针会这样移动:在 l 处于奇数块时,指针 r 不断往右移,解决所有块内的询问;l 跨越到下一块(偶数块)时,r 指针不断往左移,在返回的过程中解决按照 r 从大到小排序的询问: 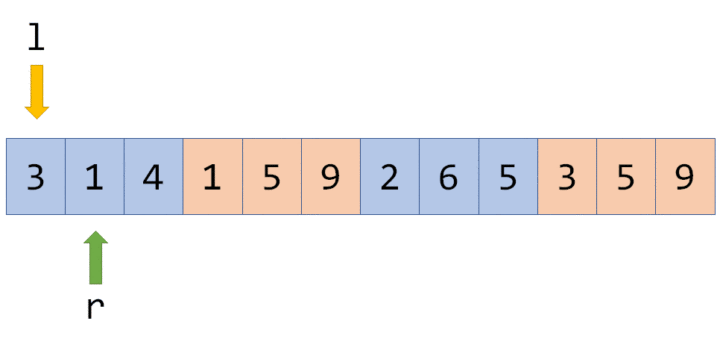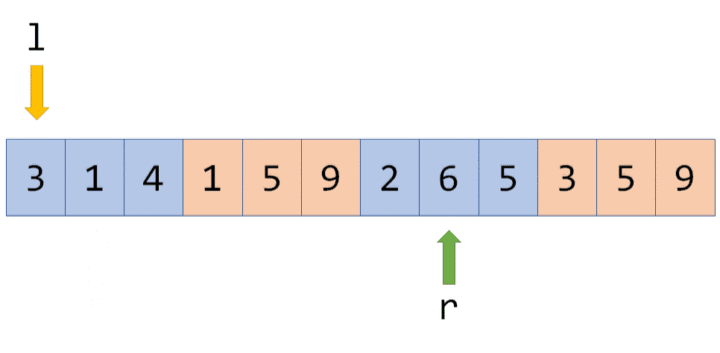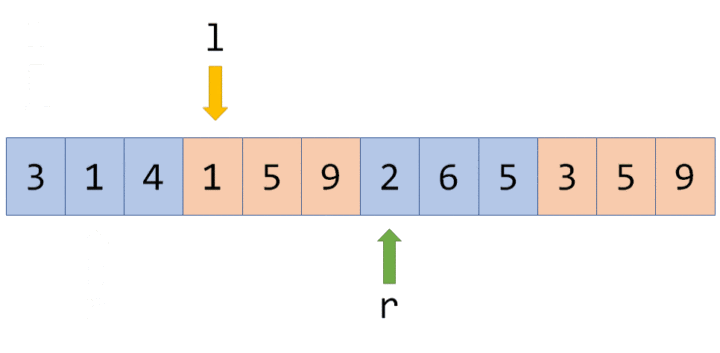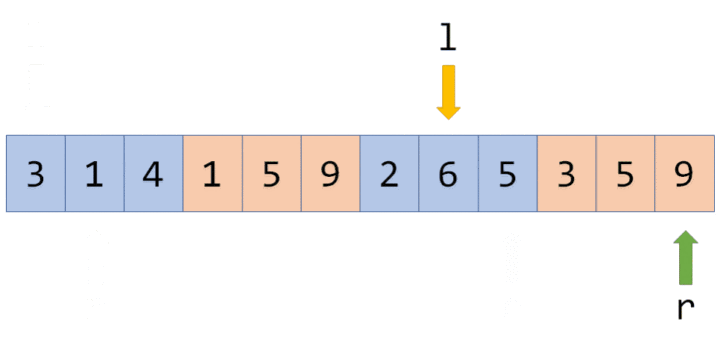
询问的结构体代码如下:
const int MAXN = 1e5 + 10;int sqr = sqrt(n);struct Q { int l, r, id; bool operator<(const Q &b) const { //重载 <运算符,奇偶化排序 只需要知道每个元素归属于哪个块,块大小为sqrt(n),所以直接l sqrt(n)即可 if (l sqr !="b.l" sqr) return l < b.l; & 1) 奇数块 r b.r;> b.r; }} Q[MAXN]; 转载地址:https://memcpy0.blog.csdn.net/article/details/108209328 如侵犯您的版权,请留言回复原文章的地址,我们会给您删除此文章,给您带来不便请您谅解!
发表评论
最新留言
关于作者
