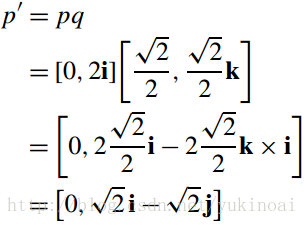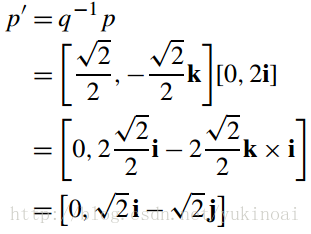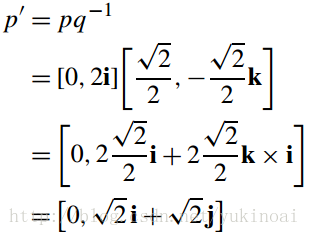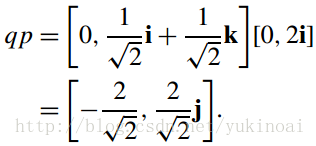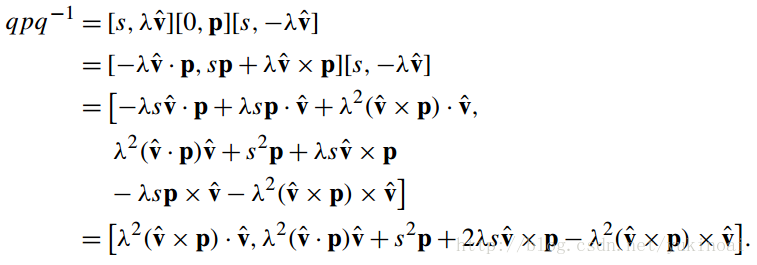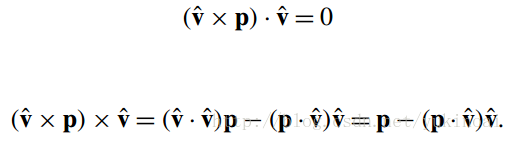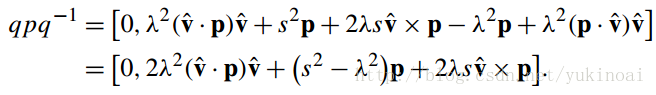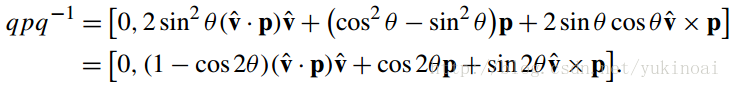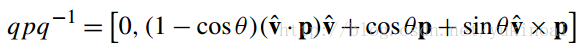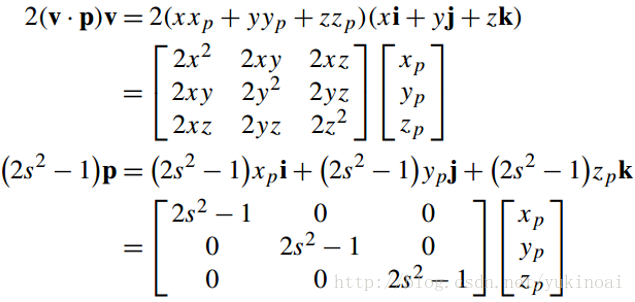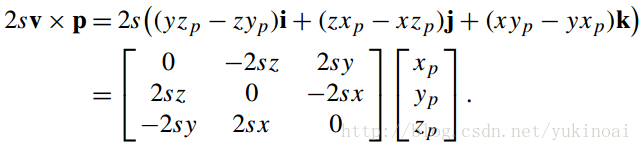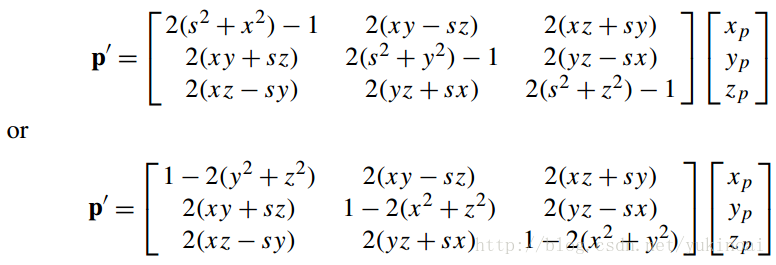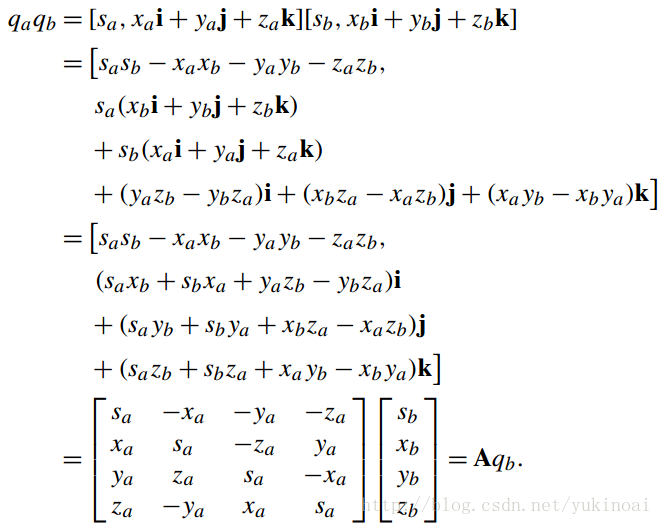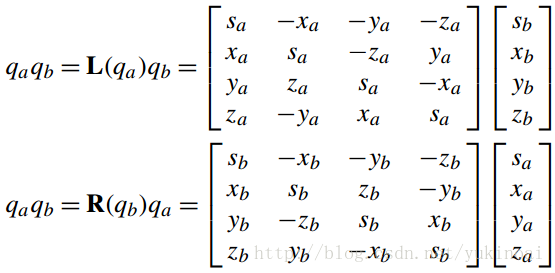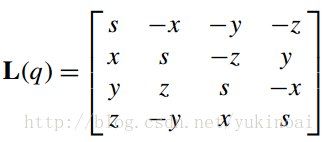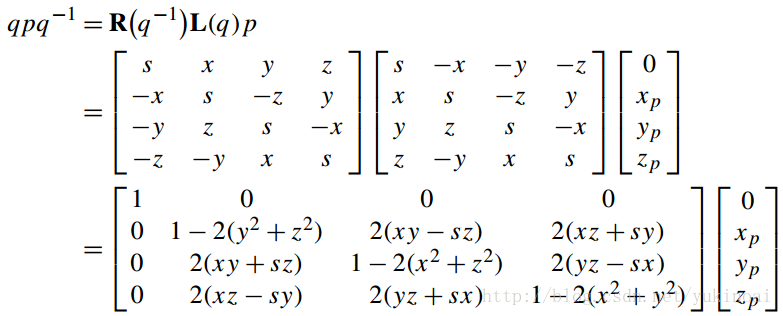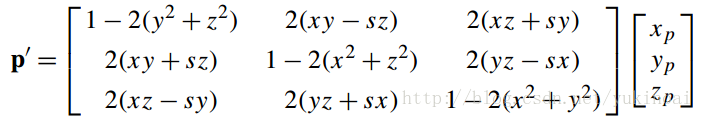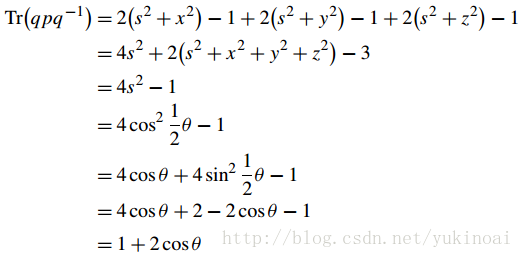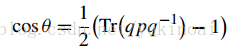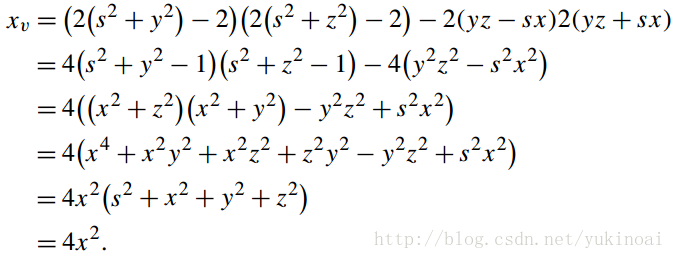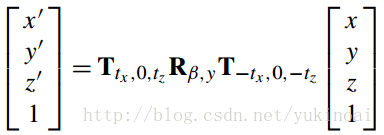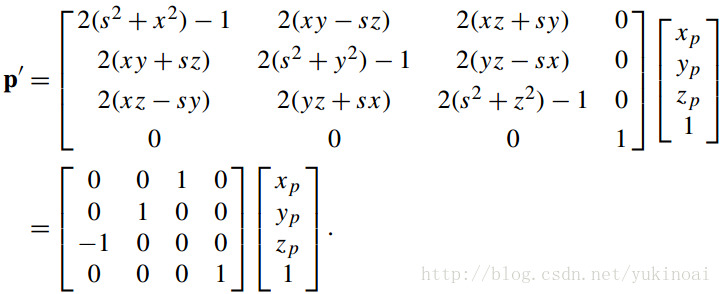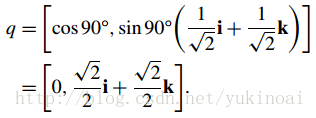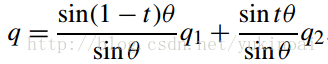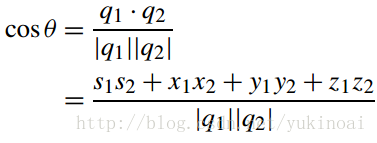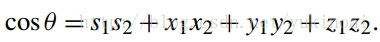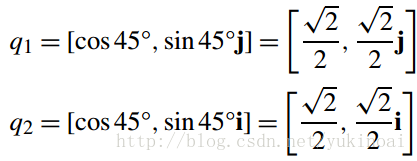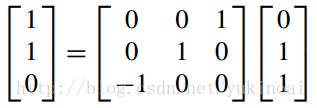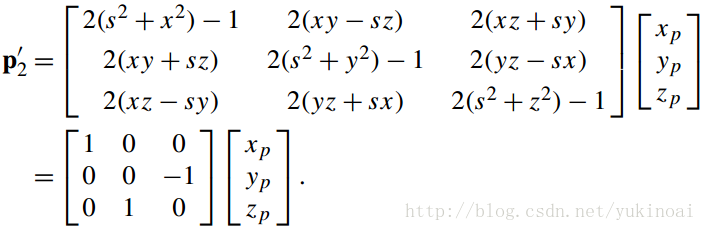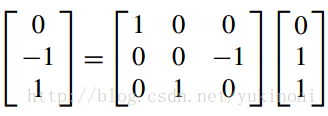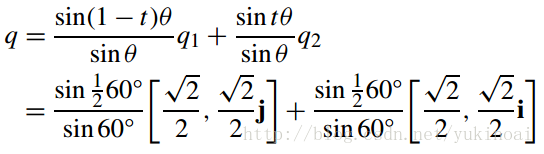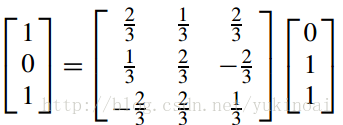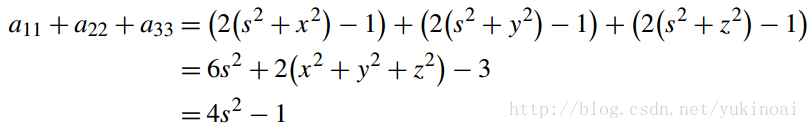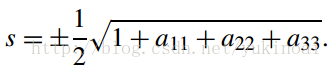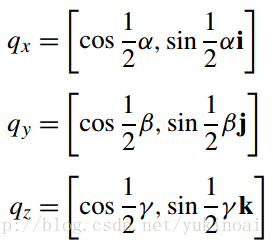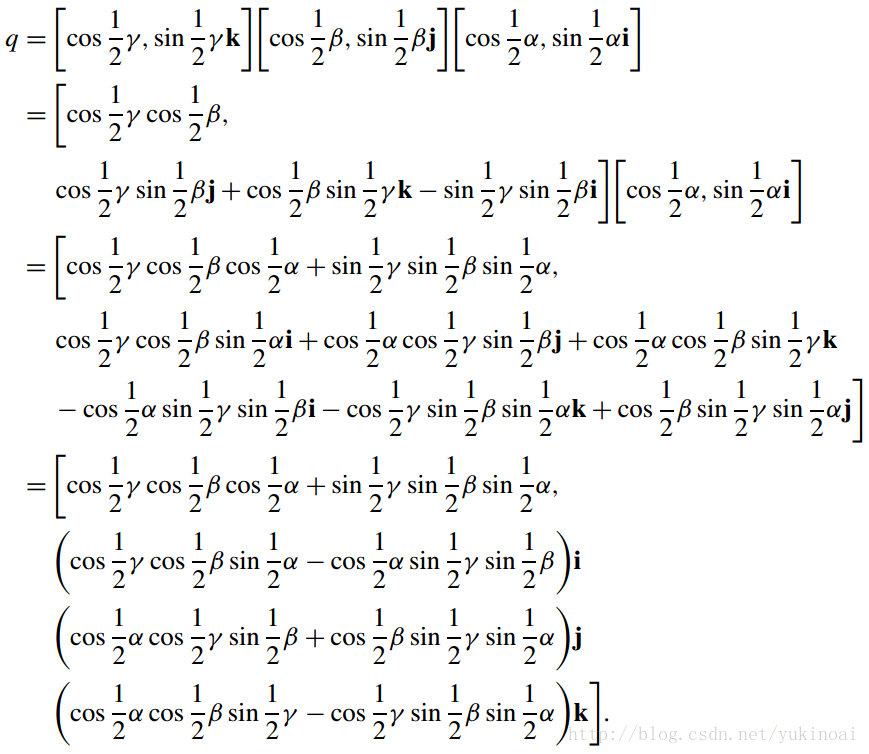本文共 5328 字，大约阅读时间需要 17 分钟。

电子书可以在这下载：

这个视频讲的很不错：

第七章  空间四元数

7.1介绍

在这一章中我们将展示如何使用四元数绕任意轴旋转矢量。我们首先回顾一些与四元数有关的的历史，特别是Benjamin Olinde Rodrigues扮演了重要角色，他发现了在旋转变换半角的重要性。

对于一个特殊的四元数，当四元数表示为

q = [cosθ, sinθv]

表示一个向量绕轴v旋转θ角。但是，正如我们将要发现的，对于三个四元数乘积，当四元数表示为

q = [cos1/2θ, sin1/2θv]

表示一个向量绕轴v旋转θ角。这半角是由罗德里格斯发现的。

在复合代数的前几章揭示了四元数是比较特殊的，并告诉我们为什么汉弥尔顿不基于超复数z = s+ai+bj去定义代数。

然后我们研究各种四元数乘法来发现它们的转动性质。从两正交四元数开始，并走向一般情况下使用qpq−1 ，其中q是单位规范四元，p是一种纯四元。

两种技术被用来作为一个矩阵表达一个四元数乘积，它依次编码特征向量和特征值。最后，我们考察四元数插值。

我们继续用一个有序对表达一个四元数，用斜体小写字母代表数，和加粗的小写字母表示向量。

7.2一些历史

略

7.3四元数乘积

 一个四元数是有一个标量s和一个向量v组成的：

q = [s, v]     s∈R, v∈R3.

如果我们把向量部分展开，则

q = [s,xi + yj + zk]      s,x,y,z∈R.

哈密顿希望四元数可以像复数一样表示表示转动，就像我们在第二章中见到的

Rθ = cosθ + i sinθ

表达了旋转θ角。单位范数的四元数q可以用来旋转吗？作为一个纯粹的四元数p存储矢量？是的，但只是在有限的意义上。为了理解这一点，我们来构造单位范数四元数q和纯四元数p的乘积。单位四元数q定义为：

q = [s,λv]    s,λ∈R, v∈R3

|v | = 1

s2 + λ2 = 1

纯四元定义为

p = [0, p]    p∈R3.

让我们来计算乘积

p’ = qp

= [s,λv ][0, p]

= [−λv · p,sp+ λv × p].

我们可以看出结果是一个有标量和向量的一般四元数。

7.3.1特殊情况

狭义的是指v必须垂直与p，这样−λv · p就会消失，而保留纯四元数：

p’ = [0,sp + λv × p].

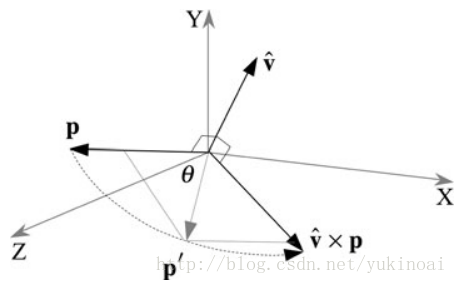
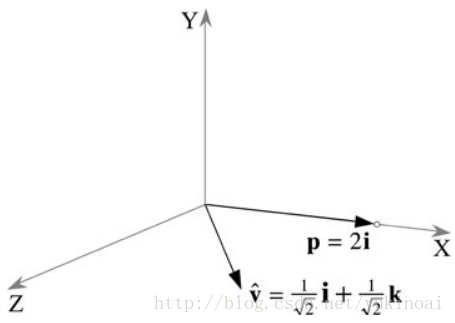
上图解释了这种情况，v垂直与p，v × p垂直与v，p组成的平面。由于v是单位向量，所以|p| = |v × p|，这意味着我们有两个长度相等的正交向量，p和v × p。因此p关于v的转动可以令s = cosθ和 λ = sinθ来表示：

p’ = [0, p’]

= [0, cosθp + sinθv ×p].

例如上图，绕z轴旋转一个矢量，如果旋转角度θ=45°。

     q = [s,λv]

= [cosθ, sinθk]

= [√2/2, √2/2k]

如果被旋转的向量为p = 2i，则

p = [0, p]= [0, 2i].

存在四种乘法组合值得思考：qp, pq, q−1p和pq−1，让我们从qp开始

p旋转45°到p’ =√2 i + √2 j

接下来尝试pq：

p旋转-45°到p’ =√2 i -√2 j

接下来尝试q-1p，

p旋转-45°到p’ =√2 i -√2 j

最后是pq-1

p旋转45°到p’ =√2 i + √2 j

因此对于正交四元数，θ是旋转角，且

qp = pq−1

pq = q−1p.

回到之前，让我们看看θ=180°乘法qp会发生什么

p’ = qp

= [−1, 0][0, 2i]

= [0,−2i]

p旋转了180°到p’ =−2i.

注意，在上述所有乘法中，向量在旋转过程中没有被缩放。这是因为q是单位范数四元数。现在让我们看看如果我们改变v和p会发生什么.我们减少到45°和保留q的单位矢量，如图下图所示。

因此，

v = 1/√2i + 1/√2k

q = [cosθ, sinθv ]

p = [0, p].

则

p’ = qp

= [cosθ, sinθv ][0,p]

= [−sinθv · p, cosθp + sinθv × p].

带入vp，并令θ=45°

不幸的是，它不再是一个纯四元数。它没有被旋转45°，且矢量的范数是减少到√3！将向量乘以非正交四元数，会将一些向量成分转换成四元数的标量中。

7.3.2一般情况

不用担心，让我们来看看他可以被逆四元数还原回去吗？

这是一个纯粹的四元数。此外，没有缩放，因为它的范数仍然是2，但是矢量已经旋转了90°而不是45°，是所需角度的两倍，如图下图所示。

如果这个“夹”在q和q−1纯四元数形式的载体是正确的，这表明增加θ到90°应转动p = 2i 180°到2k。

让我们试试这个，令θ=90°

这证实了我们的预测，表明了qpq-1的作用。现在让我们来演示这个二倍角是如何产生的。根据前面的设定

注意

因此

显然，这是一个纯粹的四元数，因为标量是零。然而，角度倍增是从哪里来的并不明显。让我们来看看当s = cosθ ，λ = sinθ会发生什么

双倍角出现了！所以如果我们希望这个乘法使向量旋转θ角，我们应该在一开始就将θ减半。

q = [cos1/2θ, sin 1/2θv]

这会使

qpq-1乘法是由哈密顿发现但未发表的结果。Cayley在1845发现了并公布结果。然而，Altmann指出，“在Cayley的论文集，他承认先于哈密顿”，这是一个很客观的事实。然而，Rodrigues在哈密顿和Cayley钱承认半角参数的重要性并发表的一个解决方案，在这之前他没有见过哈密顿。

7.4 四元数的矩阵形式

之前已经发现一个矢量方程为代表的qpq-1，让我们继续把它转换成一个矩阵。我们将探讨两个方法：第一个是一个简单的矢量方法将qpq-1直接成矩阵形式的矢量方程。第二种方法使用矩阵代数来开发一个相当巧妙的解决方案。

7.4.1向量方法

根据前面的研究我们已经得到

qpq−1 =[ 0, 2(v · p)v +( 2s2 – 1)p + 2sv ×p]

如果令p’=qpq-1则

p’ = 2(v · p)v + (2s2 – 1)p + 2sv × p.

其中2(v · p)v，(2s2 – 1)p和2sv × p可以分别表达为

这些矩阵加起来得

7.4.2矩阵法

根据第五章的知识如果有以下两个四元数

qa = [sa,xai + yaj + zak]

qb = [sb,xbi + ybj + zbk]

则它们的乘积为

也可以表示为

写成以下形式

记住L（qa）qb= R（qb）qa，这是理解下一阶段的中心。此外，如果你在第一读中不能理解，也不要感到惊讶。作者花了数小时的痛苦试图破译原始的算法，而这种解释已经扩展，以确保您不会遭受同样的体验！

首先，让我们用矩阵L和R重新排列四元数乘法qaqcqb到qaqbqc，即移动qc从中间到右边。我们开始先把四元乘法qaqcqb分为两部分，qaqc和qb。我们可以这样做，因为四元数代数是有结合律的：

根据上面的式子最终可以写为：

qaqcqb = L(qa)qcqb= R(qb)L(qa)qc

这样就达到了移动qc从中间到右边的目的。并且左边两个矩阵可以合成为一个。

下面让为我们对qpq-1做同样的操作可以得到

qpq−1 = L(q)pq−1 = R(q−1)L(q)p

下面计算q= [s,xi + yj + zk]时的矩阵R(q−1)和L(q)

则qpq−1可以写为

忽略第一行和第一列可得

这和向量法的得到的结果相同。

7.5多次旋转

表示一个向量或参照系受到q1然后是q2所指定的两个旋转。有一种转换四元数为各自的矩阵再相乘在一起。然而，这并不是最有效的转换方式。最好是旋转四元数相乘后转换为矩阵表示，因为四元数的相乘比矩阵简单一些。

7.6特征值和特征向量

虽然上式是一个旋转矩阵，但我们可以通过计算它的特征值和特征向量来获得进一步的证据。特征值应满足

Tr(qpq−1) = 1 + 2 cosθ

其中Tr是迹函数，表示矩阵主对角线元素和。

所以

为了计算特征向量，我们使用附录中的三个公式

因此

相似的得出，yv = 4y2 and zv = 4z2, 这证实，相关的特征向量与四元数向量有相同的成分。出现平方项并不奇怪，因为qpq−1是三个四元数的乘积。

7.7关于偏置轴的旋转

现在我们有一个矩阵来表示一个四元数转子，我们可以用它来解决问题，就像绕偏置轴旋转一个点。例如，在6章我们使用以下符号

表示绕一个平行于Y轴的轴旋转。如果我们用qpq-1来表示则

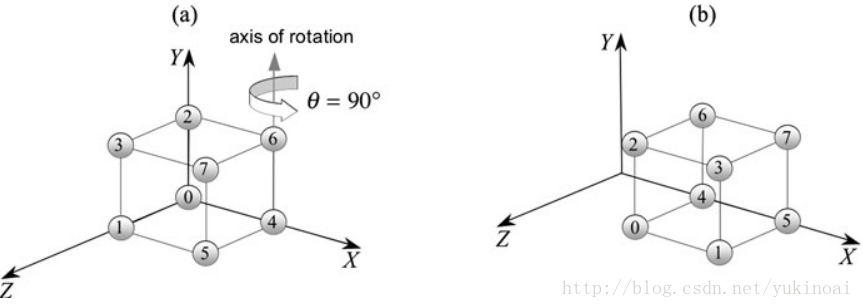
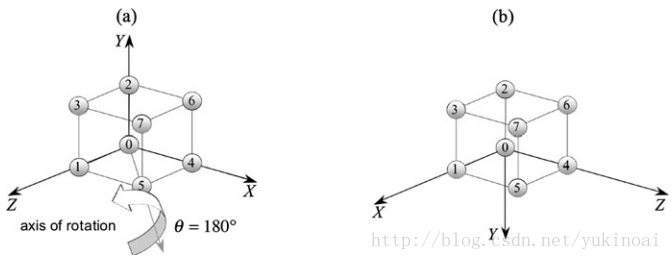
让我们用下面的立方体测试一下

可以看出

q = [cos 45°, sin 45°j

p = [0, p].

结果是

s =√2/2, x = 0, y =√2/2,z = 0

使用矩阵公式

其他两个矩阵为

三个矩阵相乘得

虽然在数学上不正确，下面的语句显示矩阵（7.19）和代表一个单元立方体的坐标数组，然后是旋转后立方体的坐标。

验证了上图的结果

7.8 参考坐标系

乘法qpq−1用于使点绕四元数q相关的向量旋转，而q−1pq可用于使点反方向旋转。但这种反向旋转也相当于参照系的变化。为了演示这一点，请考虑旋转参考系180°，如下图所示关于i +k的问题。这种旋转的单位范数四元数是

结果是

s = 0, x =√2/2, y = 0, z =√2/2

然后可以得到矩阵

与每个顶点坐标相乘可得

与图中结果相同

7.9 四元数插值

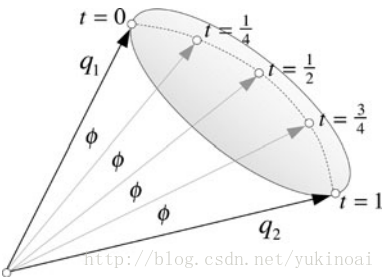
像矢量一样，四元数可以被插值。然而，鉴于两插值矢量的结果第三的向量，是很容易想象两四元数插值结果为第三四元数并作为转动算子，并不是立即可视化的。

矢量的球面插值

其中θ是两个矢量间的夹角，同理四元数插值为

所以如果给出两个四元数

q1 = [s1,x1i + y1j + z1k]

q2 = [s2,x2i + y2j + z2k]

θ可以有由两个四元数的乘积得到

如果使用单位四元数则

上图显示了一个这样的场景，其中的点（0, 1, 1）绕v1轴旋转90°。图7.12显示了另一个场景，其中相同的点（0, 1, 1）绕v2旋转90°。对应四元数是

因此cosθ=0.5，θ=60°

下面计算一下矩阵形式

 

说明四元数是正确的

下面进行插值，先取t=0.5，由插值公式可得

 

使用矩阵验证

和下图中的结果一致

使用一个球形插值的一个原因是它的线性插值两单位规范四元数之间的角度，造成他们之间的恒定角速度。然而，一个问题是四元数在四维空间中，是一个半径等于四元数模的超球体。我们的3D的大脑是很难想象的。然而，我们可以说服自己我们看到什么的一个简单的示意图，如下图所示，在这里我们看到的超球体和两个四元数q1和q2的部分。。在这个例子中，角φ是插值T之间的不变角。球形插值两值之间的恒定角也使插值四规范保持不变的统一，防止任何不必要的缩放。

下图提供了一个草图帮助想象发生了什么。例如，当T = 0，插值四元数是q1，旋转点（0, 1, 1）至（1, 1, 0），当t = 1，内插的四元数q2旋转点（0, 1, 1）到（0，−1, 1）。当t＝0.5时，插值的四元数将上面的点（0, 1, 1）旋转到（1, 0, 1）。另外两条曲线显示了T＝0.25和t＝0.75的情况。

的插值的自然结果是，T = 0，T = 1旋转的角度是90°，但T = 0.5的旋转角度（特征值）约为70.5°。t的其他值出现相应的角度。

7.10 将旋转矩阵换为四元数

有前面可知qpq-1的转换矩阵为

观察矩阵表明，通过结合各种元素我们可以隔离一个四元数的x，y，z，s，例如，通过a11 + a22 + a33得到

因此

同理

 

 

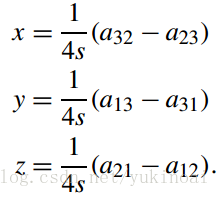
7.11 欧拉角到四元数

在6章我们发现旋转变换Rα,x，Rβ,y和Rγ,z可以产生十二种组合代表一个复合旋转。现在让我们看看这种变换是如何用四元数表示的。

为了演示该技术，我们必须选择十二个组合中的一个，然后使用相同的技术来转换其他组合。例如，让我们选择序列Rγ,z，Rβ,y和Rα,x相当于四元数

所以

则

7.12总结

本章一直是本书的焦点，单位规范四元数已被用于一个四元数的向量旋转。这是否可以通过简单的乘法qp来实现，就像复数一样。但正如我们所看到的，只有当四元数与向量正交时才起作用。乘法qpq-1用于（由哈密顿和Cayley发现）四元数和向量之间的转换。它也比较容易计算。我们还看到，该乘法可以表示为一个矩阵，它可以与其他矩阵相结合。

也许，在本章中出现的最有趣的特点就是一个四元数虚数不是任何计算所需要的，因为他们是嵌入在代数。

球形插值提供了一个动态变化的一个四元数的轴和旋转角度的聪明方法，但很难想象作为没有实时显示系统一个动画序列。

逆向乘法q-1pq逆转的旋转角度，和qpq-1相当于改变在旋转角度的标志。因此，qpq-1可用于同一方向的旋转参考系。

7.12.1操作总结

 

转载地址：https://blog.csdn.net/yukinoai/article/details/79127774 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！