本文共 2341 字，大约阅读时间需要 7 分钟。

变分法是处理泛函的数学领域，和处理函数的传统微积分相对。

传统的微积分中的一个常见的问题是找到一个$x$ 值使得 $y(x)$ 取得最大值或者最小值。类似的，变分法中，寻找一个函数 $y(x)$来最大化或者最小化泛函$F(y)$。

变分法可以用来说明两点之间的最短路径是一条直线或者最大熵分布是高斯分布。

本文介绍什么是泛函。

泛函概念

设$C$ 是一个由函数组成的集合，对于$C$ 中的任何一个元素 $y(x)$，数集 $B$ 中都有一个元素$F$ 与之对应，称 $F$ 是 $y(x)$ 的泛函（functional），记作 $F=F[y(x)]$

一般情况下,泛函式常用积分形式表示

$$J[y(x)]={\int }_{x_0}^{x_1}F(x,y,y^{\prime })dx$$

式中，被积函数 $F(x,y,y^{\prime })$称为核。

由此可见，泛函是定义域为函数集，而值域为实数或者复数的映射，换句话说，它是从函数组成的一个向量空间到标量域的映射，它的输入为函数，而输出为标量。

这里把泛函和函数、算子的概念区别理解一下：

• 算子是一个函数到另一个函数的映射，它是从向量空间到向量空间的映射
• 泛函是从向量空间到数域的映射
• 函数是从数域到数域的映射

泛函例子1——两点之间的最短路径

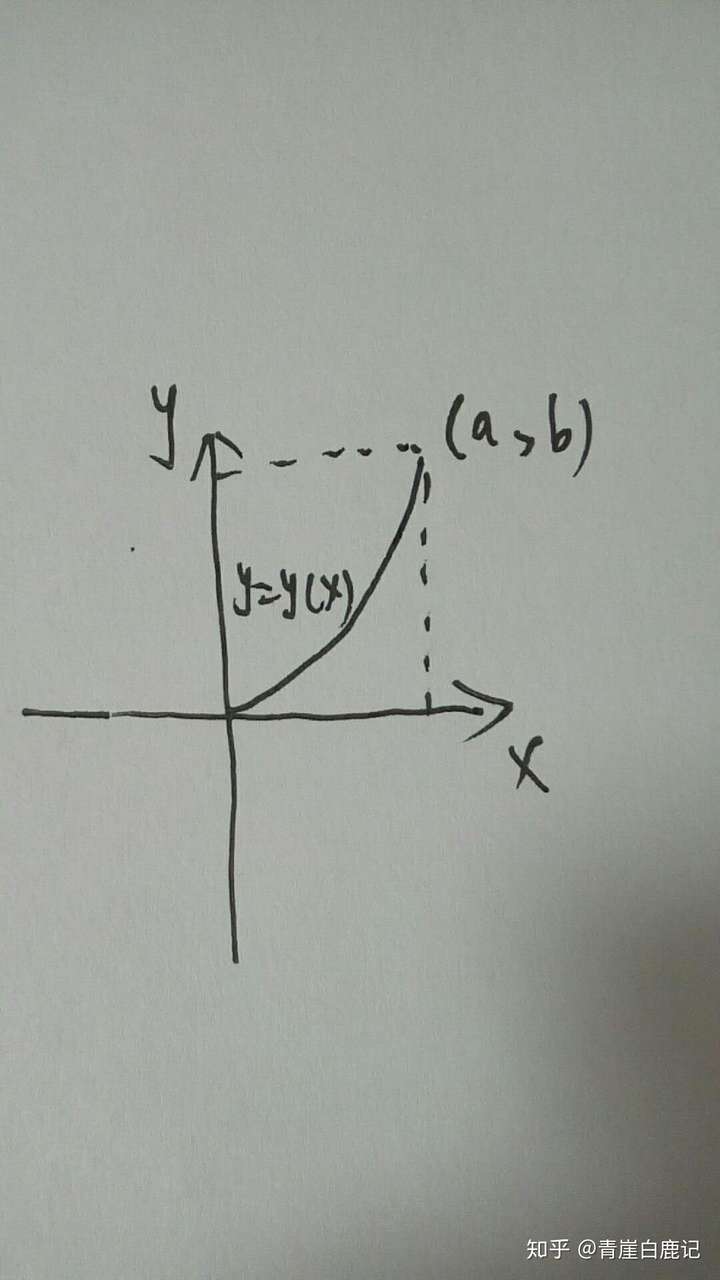
如图所示二维平面空间，从坐标原点$(0,0)$到点$(a,b)$的连接曲线是 $y=y(x)$

曲线的弧长微元是$d{s}^2=d{x}^2+d{y}^2$或者$ds=\sqrt{1+(\frac{dy}{dx}{)}^2}dx$

曲线的总弧长是:

$$s={\int }_0^a(1+y^{\prime 2}{)}^{\frac{1}{2}}dx$$

其中$s$是标量，上式右边是 $y^{\prime }(x)$ 的广义函数，被称为泛函，可记为 s(y’)

问题变成了：找出曲线$y(x)$，使得泛函 $s(y^{\prime })$ 最小。

这个问题可以用变分法求解。

泛函例子2——最速降线问题

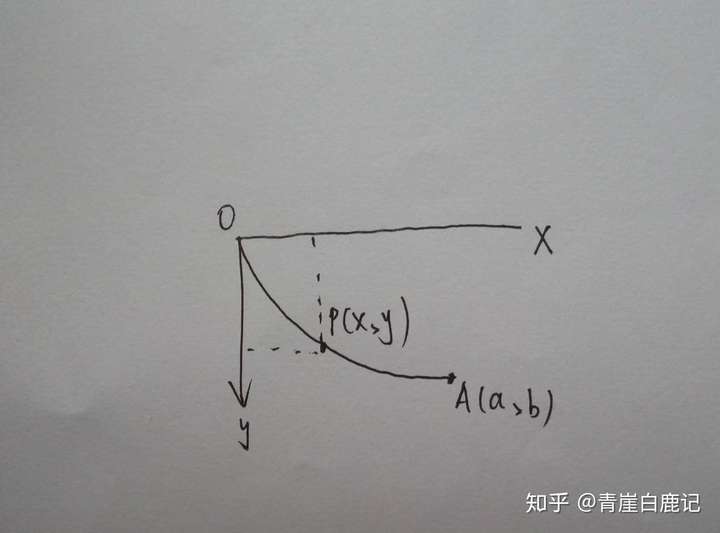
如图所示，设 O, A 是高度不同，且不在同一铅垂线上的两定点，有一重物沿去曲线从O到A受重力作用自由下滑。若忽略摩擦力和阻力，那么曲线是哪种形状时质点降落的时间最短？

当重物从O到运动曲线上的一点P时，失去的势能是 $mgy$，获得的动能是 $\frac{m{v}^2}{2}$ ，由能量守恒：

$$v^2=2gy$$

在曲线上点 $(x,y)$ 处，重物的运动速度为：

$$v=\frac{ds}{dt}=\frac{\sqrt{1+y^{\prime 2}}dx}{dt}$$

其中 s 表示曲线的弧长, t 表示时间，那么：

$$dt=\frac{\sqrt{(1+y^{\prime 2})}dx}{v}=\frac{\sqrt{(1+y^{\prime 2})}dx}{2gy}$$

则 m 从 O 点运动到 A 点所需时间为：

$$t=J(y)={\int }_0^a\frac{\sqrt{(1+y^{\prime 2})}dx}{2gy}$$

重物由 O 点运动到 A 点所需时间$t$ 是 $y(x)$的函数，也就是说最速降线问题是满足条件 $y(0)=0,y(a)=b$ 的所有连续函数 $y(x)$ 中，求出一个函数 $y$ 使 取最小值。

泛函例子3——信息熵

在机器学习领域，广泛被使用的泛函是连续变量 x 的熵 H[x] ，因为对于任意概率密度函数 p(x) ,它都返回一个标量值表示这个概率密度下 x 的熵。 因此，p(x)的熵写成 H[p] 也可以：

$$H[p]=-\int p(x)lnp(x)dx$$

转载自：

转载地址：https://jensen-lee.blog.csdn.net/article/details/89096756 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！