本文共 8576 字，大约阅读时间需要 28 分钟。

本文是变分法理解系列的第2篇文章，第一篇文章见变分法理解1——泛函简介，本文的要点如下：

• 基本概念
• 两个引理
• 什么是函数的变分
• 什么是泛函的变分
• 欧拉-拉格朗日方程（Euler–Lagrange equation）的证明

基本概念

具有某种共同性质的函数构成的集合称为类函数，记作F。例如在最速降线例子中的所有曲线都通过点O和A，通过点O和A就是函数集合具有的共同性质。

如果一个类函数中的某个函数能够使某个泛函取得极值或可能取得极值，则该类函数称为变分问题的可取类函数。可取类函数中的函数有无穷多个，其中任何一个都称为可取函数。

类函数中能使泛函取得极值或可能取得极值的函数或曲线称为极值函数，也称为变分问题的解。

变分法的核心问题就是求解泛函的极值函数和极值函数对应的泛函极值。

如果可取曲线类的曲线端点预先给出且为定值，则所求泛函极值的问题称为固定端点变分问题。

引理

引理1

如果函数 $f(x)$ 在$[a,b]$内连续， $\eta (x)$ 是满足 $\eta (a)=\eta (b)=0$ 的任意函数，如果

$${\int }_a^{b}f(x)\eta (x)dx=0$$

成立，那么对于所有的$x\in [a,b]$,有$f(x)\equiv 0$

证明：

反证法，设f(x)不恒为0

由 $\eta (x)$ 的任意性，取 $\eta (x)=-f(x)(x-a)(x-b)$ ，$x$是$a$和$b$之间变动的变量，所以$(x-a)(x-b)$为负，由$f(x$)不恒为0，有：

$${\int }_a^{b}f(x)\eta (x)dx={\int }_a^b-f(x{)}^2(x-a)(x-b)>0$$

与条件矛盾，所以$f(x)\equiv 0$

引理2

如果函数 $f(x),g(x)$在$[a,b]$内连续， $\eta (x),\xi (x)$ 是满足 $\eta (a)=\eta (b)=0$ 且 $\xi (a)=\xi (b)=0$ 的任意函数，如果

$${\int }_a^b[f(x)\eta (x)+g(x)\xi (x)]dx=0$$

成立，那么对于所有的 $x\in [a,b]$ ，有 $f(x)\equiv g(x)\equiv 0$ 。

证明：

反证法，设f(x)和g(x)不恒为0

由 $\eta (x),\xi (x)$ 的任意性，取 $\eta (x)=-f(x)(x-a)(x-b),\xi (x)=-g(x)(x-a)(x-b)$，$x$是$a$和$b$之间变动的变量，所以$(x-a)(x-b)$为负，则：

$${\int }_a^b[f(x)\eta (x)+g(x)\xi (x)]dx={\int }_a^b[f(x{)}^2+g(x{)}^2][-(x-a)(x-b)]dx>0$$

这与条件矛盾，所以$f(x)\equiv g(x)\equiv 0$

函数的变分

对于任意定值 $x\in [x_0,x_1]$ ，可取函数$y(x)$ 与另一可取函数 $y_0(x)$之差 $y(x)-y_0(x)$ 称为函数$y(x)$ 在 $y_0(x)$处的变分或者叫函数的变分，记作 $\delta y$ ，其中 $\delta$ 称为变分算子，那么

$$\delta y=y(x)-y_0(x)=ϵ\eta (x)$$

关于 $ϵ\eta (x)$ 下文会详细讲

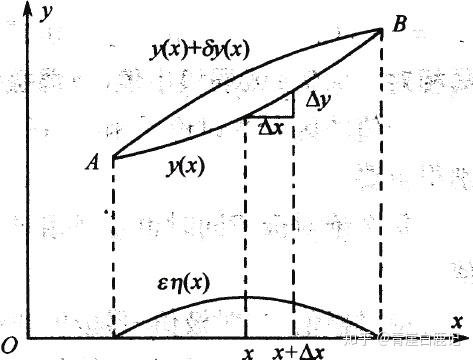
• 函数的变分 $\delta y$ 是两个不同的函数$y(x)$ 和$y_0(x)$ 在自变量x固定时的差，这是函数发生了改变。
• 函数的增量 $\Delta y$ 是自变量x的增量使得函数 $y(x)$ 产生的增量，函数依然是原来的函数。

最简泛函的变分

设 $F(x,y(x),y^{\prime }(x))$ 是三个独立变量 $x,y(x),y^{\prime }(x)$ 在区间 $[x_0,x_1]$ 上的已知函数，且二阶连续可微，其中 $y(x)$ 和 $y^{\prime }(x)$ 是$x$的未知函数，则泛函：

$$J[y(x)]={\int }_{x_0}^{x_1}F(x,y(x),y^{\prime }(x))dx$$

被称为最简泛函，被积函数F成为泛函的核。

在 $y=y(x)$ 的一阶邻域内，任取一曲线 $y=y_1(x)$ ，则：

$$\delta y=y_1(x)-y(x),{\delta }_y^{\prime }=y_1^{\prime }(x)-y^{\prime }(x)$$

由泰勒展开式，最简泛函 $J[y(x)]$的增量为：

$$\begin{array}{rl}△J& =J[y_1(x)]-J[y(x)]=J[y(x)+\delta y]-J[y(x)]\\ & ={\int }_{x_0}^{x_1}[F(x,y)+\delta y,y^{\prime }+\delta y^{\prime })dx-{\int }_{x_0}^{x_1}F(x,y,y^{\prime })dx\\ & ={\int }_{x_0}^{x_1}[F(x,y+\delta y,y^{\prime }+\delta y^{\prime })-F(x,y,y^{\prime })]dx\\ & ={\int }_{x_0}^{x_1}(F_y\delta y+F_{y^{\prime }}\delta y^{\prime })dx+\cdots +{\int }_{x_0}^{x_1}[\frac{1}{n!}(\delta y\frac{\partial }{\partial y}+\delta y^{\prime }\frac{\partial }{\partial y^{\prime }}{)}^{n}F]dx+R_n\end{array}$$

把${\int }_{x_0}^{x_1}(F_y\delta y+F_{y^{\prime }}\delta y^{\prime })dx$ 称为泛函的变分，记作 $\delta J$

Euler–Lagrange equation

回顾变分法理解1——泛函简介中的最速降线问题：

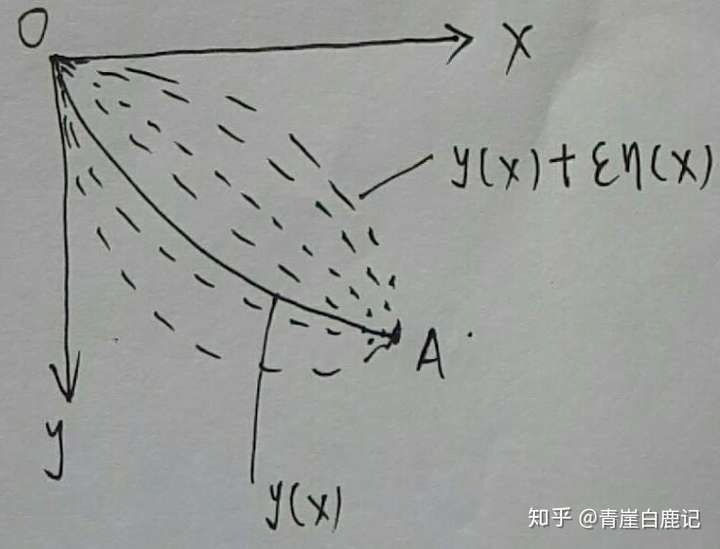
设 $\tilde{y}(x)$ 是一个可取类函数，即图中所有实线和虚线的集合。

在可取类函数 $\tilde{y}(x)$ 中存在一个二阶可微的极值函数$y(x)$（图中的实线）使得重物从O到A点的时间最短，即$y(x)$可以使泛函 $t=J[\tilde{y}(x)]={\int }_0^a\sqrt{\frac{(1+(\tilde{y}{)}^{\prime 2})}{2g\tilde{y}}}dx$ 取得极值。

可以用y(x)表示可取类函数中的所有曲线：

$$\tilde{y}(x)=y(x)+\delta y=y(x)+ϵ\eta (x)$$

其中 $ϵ$ 为Lagrange引入的实数， $\eta (x)$ 是满足 $\eta (x_0)=\eta (x_1)=0$ 的可微函数，可以看出在 $ϵ=0$ 时 $\tilde{y}(x)=y(x)$ ，使泛函 $t=J[\tilde{y}(x)]={\int }_0^a\sqrt{\frac{(1+(\tilde{y}{)}^{\prime 2})}{2g\tilde{y}}}dx$ 取得极值为 $J[y(x)]$。

泛函 $J[\tilde{y}(x)]$ 可以表示为：

$$\varphi (ϵ)=J[\tilde{y}(x)]=J[y(x)+ϵ\eta (x)]={\int }_{x_0}^{x_1}F(x,y(x)+ϵ\eta (x),y^{\prime }(x)+ϵ{\eta }^{\prime }(x))dx$$

式是一个关于 x 积分式，在求解积分之后，剩下的只有 $ϵ$ ，因此它其实是 $ϵ$ 的函数，这个函数的特性是在$ϵ=0$ 时取得极值$J[y(x)]$，也就是在 $ϵ=0$ 时， $\varphi (ϵ)$ 满足：

$$\frac{d\varphi }{dϵ}{|}_{ϵ=0}=0$$

由求导与积分顺序的可交换性， $\frac{d\varphi }{dϵ}$ 形式如下：

$$\begin{gathered} \frac{d\varphi }{dϵ}={\int }_{x_0}^{x_1}{F}_y[x,y(x)+ϵ\eta (x),y^{\prime }(x)+ϵ{\eta }^{\prime }(x)]\eta (x) \\ +F_{y^{\prime }}[x,y(x)+ϵ\eta (x),y^{\prime }(x)+ϵ{\eta }^{\prime }(x)]{\eta }^{\prime }(x)dx \end{gathered}$$

令 $ϵ=0$ ：

$$\frac{d\varphi }{dϵ}{|}_{ϵ=0}={\int }_{x_0}^{x_1}[F_y\eta (x)+F_{y^{\prime }}{\eta }^{\prime }(x)]dx=0$$

应用分部积分法

$$\begin{array}{rl}0& ={\int }_{x_0}^{x_1}[F_y\eta (x)+F_{y^{\prime }}{\eta }^{\prime }(x)]dx\\ & ={\int }_{x_0}^{x_1}{F}_y\eta (x)dx+{\int }_{x_0}^{x_1}{F}_{y^{\prime }}{\eta }^{\prime }(x)dx\\ & =F_y\eta (x)dx+{\int }_{x_0}^{x_1}{F}_{y^{\prime }}d\eta (x)\\ & =F_y\eta (x)dx+F_{y^{\prime }}\eta (x){|}_{x_0}^{x_1}-{\int }_{x_0}^{x_1}\eta (x)(\frac{d}{dx}{F}^{\prime }y)dx\\ & ={\int }_{x_0}^{x_1}(F_y-\frac{d}{dx}{F}^{\prime }y)\eta (x)dx+F_{y^{\prime }}\eta (x){|}_{x_0}^{x_1}\end{array}$$

由于 $\eta (x_0)=\eta (x_1)=0$ ，因此： $F_{y^{\prime }}\eta (x){|}_{x_0}^{x_1}=0$

推出：

$${\int }_{x_0}^{x_1}(F_y-\frac{d}{dx}{F}^{\prime }y)\eta (x)dx$$

再由引理1：

$$F_y-\frac{d}{dx}{F}^{\prime }y=0$$

Euler–Lagrange equation也可以利用泛函取得极值时， $\delta J=0$ 来证明。

$\eta (x)$ 实际上是加在y(x)上一个扰动，Euler–Lagrange equation的意义在于不管扰动是什么形式，如果泛函取得极值，都有 $F_y-\frac{d}{dx}{F}_y^{\prime }=0$成立。

转载自：

转载地址：https://jensen-lee.blog.csdn.net/article/details/89148553 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！