数据结构与算法：17 图

发布日期：2021-06-30 22:50:26 浏览次数：2 分类：技术文章

本文共 24510 字，大约阅读时间需要 81 分钟。

17 图

知识结构：

图1 知识结构

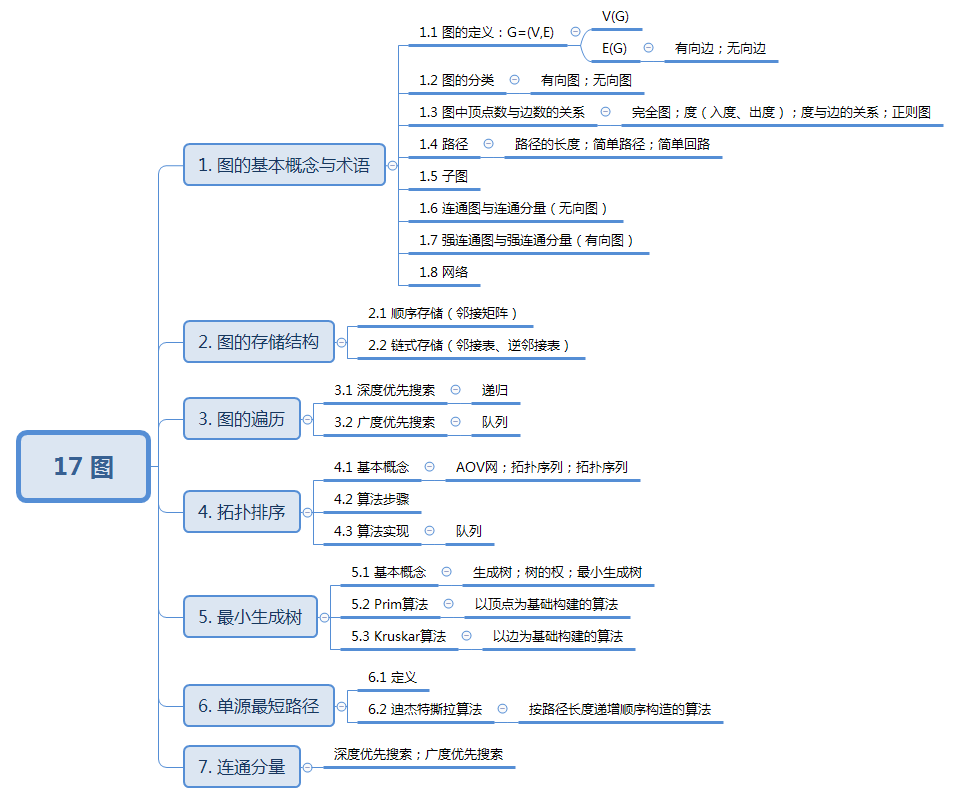
1. 图的基本概念与术语

1.1 图的定义

图由顶点集和边集组成，记为 $G = (V, E)$ 。

顶点集：顶点的有穷非空集合，记为 $V (G)$ 。

边集：顶点偶对的有穷集合，记为 $E (G)$ 。

边：

无向边： $v_i,v_j)=(v_j,v_i)$

有向边（弧）： $<v_i,v_j> \neq <v_j,v_i>$ 始点 $v_i$ 称为弧尾，终点 $v_j$ 称为弧头。

例题：

图2 图的表示

例题：

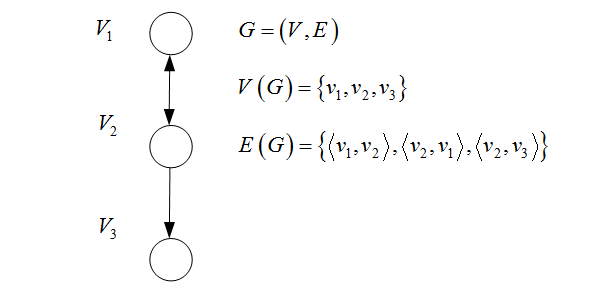
图3 图的表示

1.2 图的分类

有向图： $E (G)$ 由有向边构成。

无向图： $E (G)$ 由无向边构成。

1.3 图中顶点数与边数的关系

（1）设顶点数为 $n$ ，边数为 $e$ 则：

无向图： $0\leq e \leq \frac{n(n-1)}{2}$ ， $e=\frac{n(n-1)}{2}$ 的图称为无向完全图。

有向图： $0\leq e \leq n(n-1)$ ， $e = n (n - 1)$ 的图称为有向完全图。

（2）顶点的度

无向图： $D (v) =$ 与 $v$ 连接的边数。

有向图： $D (v) = I D (v) + O D (v)$
- $I D (v)$ ：以 $v$ 为终点（弧头）的边数。
- $O D (v)$ ：以 $v$ 为起点（弧尾）的边数。

（3）度与边的关系

$e=\frac{\sum_{i=1}^{n}D(v_i)}{2}$

（4）正则图：所有顶点的度都相同的图

图4 正则图

1.4 路径

（1）定义：图 $G = (V, E)$ ，若存在一个顶点序列 $v_p,v_{i1},v_{i2},\cdots,v_{im},v_q$ ，使得 $(v_p,v_{i1}),(v_{i1},v_{i2}),\cdots,(v_{im},v_q)\in E(G)$ （无向图）或者 $<v_p,v_{i1}>,<v_{i1},v_{i2}>,\cdots,<v_{im},v_q>\in E(G)$ （有向图）则称 $v_p$ 到 $v_q$ 存在一条路径。

（2）路径的长度：路径上边的数目。

（3）简单路径：若一条路径上除 $v_p$ ， $v_q$ 可相同外，其余顶点均不相同的路径。

（4）简单回路： $v_p$ 与 $v_q$ 相同的简单路径。

1.5 子图

设 $G = (V, E)$ 是一个图，若 $V'\subseteq V$ ， $E'\subseteq E$ 且 $E^{'}$ 中的边所关联的顶点 $\in V'$ ，则 $G^{'} = (V^{'}, E^{'})$ 也是一个图，并称其为 $G$ 的子图。

图5 图与子图

1.6 连通图与连通分量（无向图）

连通图：无向图 $G$ 的 $V (G)$ 中，任何两个顶点都存在路径，则称 $G$ 为连通图。

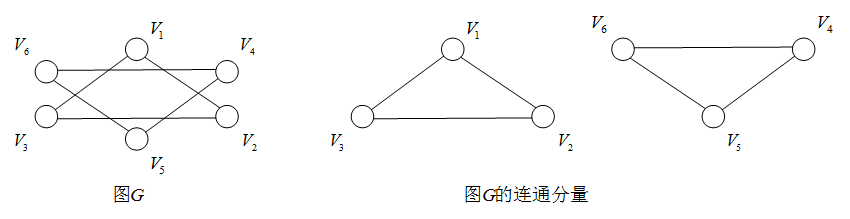
连通分量：无向图 $G$ 的极大连通子图。

注：

连通图的连通分量只有一个，为其本身。

非连通图的连通分量不唯一。

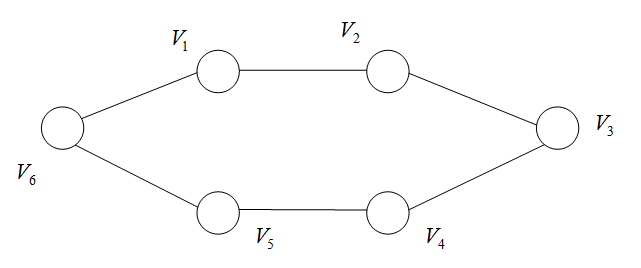
例子：

图6 连通图与连通分量

1.7 强连通图与强连通分量（有向图）

强连通图：有向图 $G$ 的 $V (G)$ 中，任何两个顶点都存在路径，则称 $G$ 为强连通图。

强连通分量：有向图 $G$ 的极大连通子图。

注：

强连通图的强连通分量只有一个，为其本身。

非强连通图的强连通分量不唯一。

例子：

图7 强连通图与强联通分量

1.8 网络

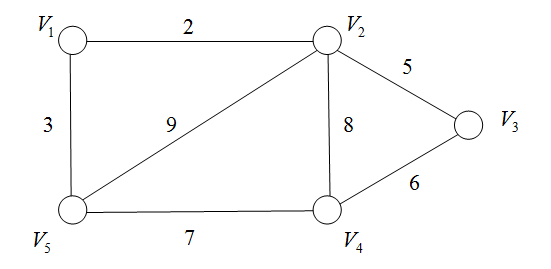
$E (G)$ 中的每条边都带有权值的图称为网络。

注：权一般具有实际意义，比如距离、消耗等。

例子：

图8 网络

2. 图的存储结构

2.1 顺序存储（邻接矩阵）

邻接矩阵：表示顶点之间相邻关系的矩阵

若图 $G = (V, E)$ ，则其邻接矩阵可表示为：

$A[i,j]==\begin{cases} 1, & (v_i,v_j)\in E(G) or <v_i,v_j>\in E(G)\\ 0, & (v_i,v_j)\notin E(G) or <v_i,v_j>\notin E(G) \end{cases}$

1,0,(vi,vj)∈E(G)or<vi,vj>∈E(G)(vi,vj)∈/E(G)or<vi,vj>∈/E(G)

例子：无向图的存储

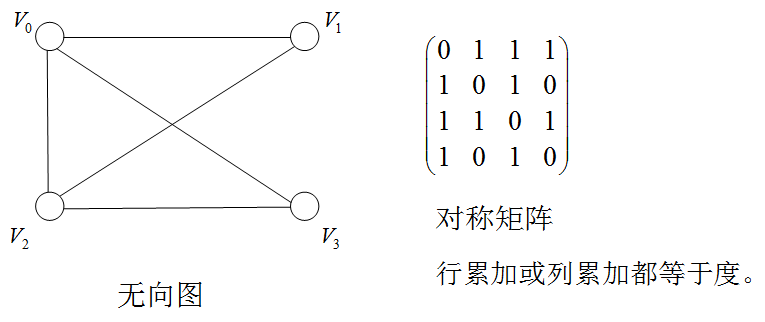
图9 邻接矩阵存储无向图

例子：有向图的存储

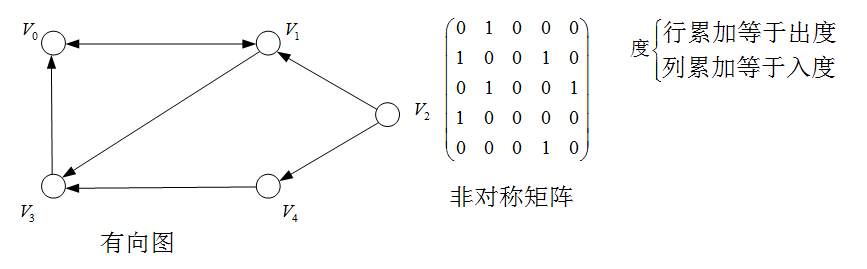
图10 邻接矩阵存储有向图

若图 $G = (V, E)$ 为网络，则其邻接矩阵可表示为：

$A[i,j]==\begin{cases} \omega_{ij}, & (v_i,v_j)\in E(G) or <v_i,v_j>\in E(G)\\ 0 or \infty, & (v_i,v_j)\notin E(G) or <v_i,v_j>\notin E(G) \end{cases}$

ωij,0or∞,(vi,vj)∈E(G)or<vi,vj>∈E(G)(vi,vj)∈/E(G)or<vi,vj>∈/E(G)

例子：网络的存储

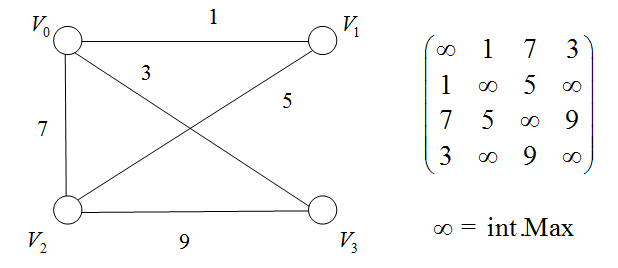
图11 邻接矩阵存储网络

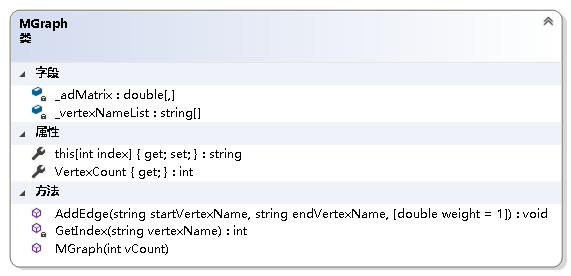
图12 MGraph结构

using System;namespace NonLinearStruct.Graph{
       ///     /// 图抽象数据类型实现--利用邻接矩阵    /// 
    public class MGraph    {
           private readonly double[,] _adMatrix;//邻接矩阵        private readonly string[] _vertexNameList;//存储图中各结点名字的数组        ///         /// 获取图中结点的个数        /// 
        public int VertexCount {
    get; }        ///         /// 初始化MGraph类的新实例        /// 
        /// 图中结点的个数        public MGraph(int vCount)        {
               if (vCount <= 0)                throw new ArgumentOutOfRangeException();            VertexCount = vCount;            _vertexNameList = new string[vCount];            _adMatrix = new double[vCount, vCount];        }                ///         /// 获取或设置图中各结点的名称        /// 
        /// 结点名称从零开始的索引        /// 
   
    指定索引处结点的名称
           public string this[int index]        {
               get            {
                   if (index < 0 || index > VertexCount - 1)                    throw new IndexOutOfRangeException();                return _vertexNameList[index];            }            set            {
                   if (index < 0 || index > VertexCount - 1)                    throw new IndexOutOfRangeException();                _vertexNameList[index] = value;            }        }                private int GetIndex(string vertexName)        {
               //根据结点名字获取结点在数组中的下标            int i;            for (i = 0; i < VertexCount; i++)            {
                   if (_vertexNameList[i] == vertexName)                    break;            }            return i == VertexCount ? -1 : i;        }                ///         /// 给邻接矩阵赋值        /// 
        /// 起始结点的名字        /// 终止结点的名字        /// 边上的权值或连接关系        public void AddEdge(string startVertexName, string endVertexName, double weight = 1)        {
               int i = GetIndex(startVertexName);            int j = GetIndex(endVertexName);            if (i == -1 || j == -1)                throw new Exception("图中不存在该边.");            _adMatrix[i, j] = weight;        }    }}

2.2 链式存储（邻接表）

邻接表：由顺序存储的顶点表和链式存储的边表构成的图的存储结构。

例子：无向图的存储

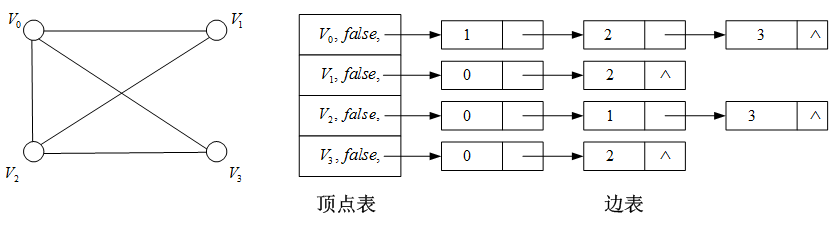
图13 无向图的存储

例子：有向图的存储

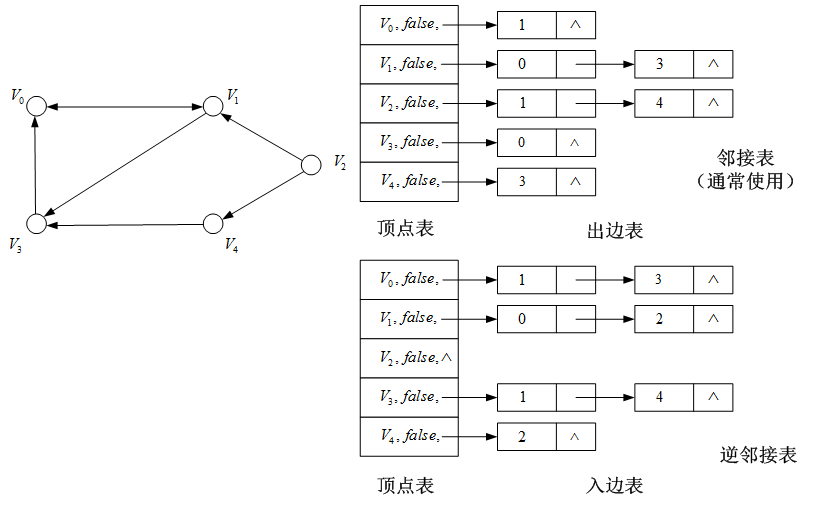
图14 有向图的存储

例子：网络的存储

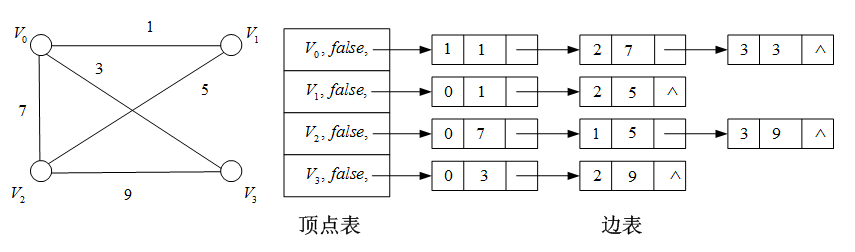
图15 网络的存储

边表结点的实现：

图16 边表结点结构

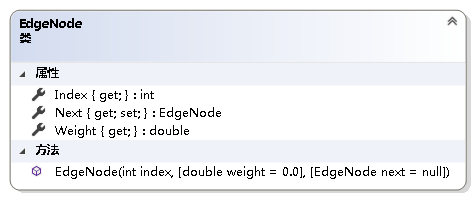
图17 EdgeNode结构

using System;namespace NonLinearStruct.Graph{
       ///     /// 邻接表边表上的结点    /// 
    public class EdgeNode    {
           ///         /// 获取边终点在顶点数组中的位置        /// 
        public int Index {
    get; }        ///         /// 获取边上的权值        /// 
        public double Weight {
    get; }        ///         /// 获取或设置下一个邻接点        /// 
        public EdgeNode Next {
    get; set; }        ///         /// 初始化EdgeNode类的新实例        /// 
        /// 边终点在顶点数组中的位置        /// 边上的权值        /// 下一个邻接点        public EdgeNode(int index, double weight = 0.0, EdgeNode next = null)        {
               if (index < 0)                throw new ArgumentOutOfRangeException();            Index = index;            Weight = weight;            Next = next;        }    }}

顶点表结点的实现：

图18 顶点表结点结构

图19 VertextNode结构

namespace NonLinearStruct.Graph{
       ///     /// 邻接表顶点表中的结点    /// 
    public class VertexNode    {
           ///         /// 获取或设置顶点的名字        /// 
        public string VertexName {
    get; set; }        ///         /// 获取或设置顶点是否被访问        /// 
        public bool Visited {
    get; set; }        ///         /// 获取或设置顶点的第一个邻接点        /// 
        public EdgeNode FirstNode {
    get; set; }        ///         /// 初始化VertexNode类的新实例        /// 
        /// 顶点的名字        /// 顶点的第一个邻接点        public VertexNode(string vName, EdgeNode firstNode = null)        {
               VertexName = vName;            Visited = false;            FirstNode = firstNode;        }    }}

图结构的实现

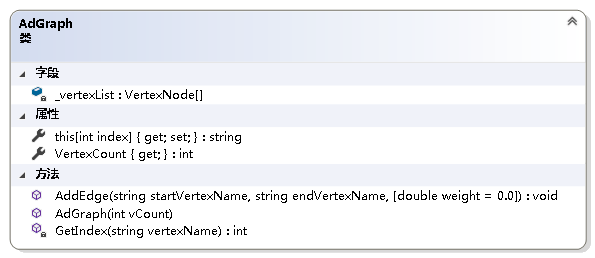
图20 AdGraph结构

using System;using System.Collections.Generic;using System.Linq;using LinearStruct;namespace NonLinearStruct.Graph{
       ///     /// 图抽象数据类型实现--利用邻接表    /// 
    public class AdGraph    {
           private readonly VertexNode[] _vertexList; //结点表        ///         /// 获取图的结点数        /// 
        public int VertexCount {
    get; }        ///         /// 初始化AdGraph类的新实例        /// 
        /// 图中结点的个数        public AdGraph(int vCount)        {
               if (vCount <= 0)                throw new ArgumentOutOfRangeException();            VertexCount = vCount;            _vertexList = new VertexNode[vCount];        }        ///         /// 获取或设置图中各结点的名称        /// 
        /// 结点名称从零开始的索引        /// 
   
    指定索引处结点的名称
           public string this[int index]        {
               get            {
                   if (index < 0 || index > VertexCount - 1)                    throw new ArgumentOutOfRangeException();                return _vertexList[index] == null                    ? "NULL"                    : _vertexList[index].VertexName;            }            set            {
                   if (index < 0 || index > VertexCount - 1)                    throw new ArgumentOutOfRangeException();                if (_vertexList[index] == null)                    _vertexList[index] = new VertexNode(value);                else                    _vertexList[index].VertexName = value;            }        }        ///         /// 得到结点在结点表中的位置        /// 
        /// 结点的名称        /// 
   
    结点的位置
           private int GetIndex(string vertexName)        {
               int i;            for (i = 0; i < VertexCount; i++)            {
                   if (_vertexList[i] != null && _vertexList[i].VertexName == vertexName)                    break;            }            return i == VertexCount ? -1 : i;        }        ///         /// 给图加边        /// 
        /// 起始结点的名字        /// 终止结点的名字        /// 边上的权值        public void AddEdge(string startVertexName, string endVertexName, double weight = 0.0)        {
               int i = GetIndex(startVertexName);            int j = GetIndex(endVertexName);            if (i == -1 || j == -1)                throw new Exception("图中不存在该边.");            EdgeNode temp = _vertexList[i].FirstNode;            if (temp == null)            {
                   _vertexList[i].FirstNode = new EdgeNode(j, weight);            }            else            {
                   while (temp.Next != null)                    temp = temp.Next;                temp.Next = new EdgeNode(j, weight);            }        }    }}

3. 图的遍历

3.1 深度优先搜索

算法：

假设 $G = (V, E)$ 以 $S$ 为起点（源点）进行搜索。

首先标识 $S$ 为已访问结点，接着寻找与 $S$ 相邻的结点 $\omega$ ，若 $\omega$ 是未被访问结点，则以 $\omega$ 为起点进行深度优先搜索，若 $\omega$ 是已被访问结点，则寻找其它与 $S$ 相邻的结点，直到与 $S$ 有路径相通的所有结点都被访问过。

例子：

图21 图的结构

深度优先搜索的序列为： $V_0,V_1,V_3,V_7,V_4,V_5,V_2,V_6$

虽然遍历序列不唯一，但是邻接表确定后，遍历序列就唯一了。

实现：

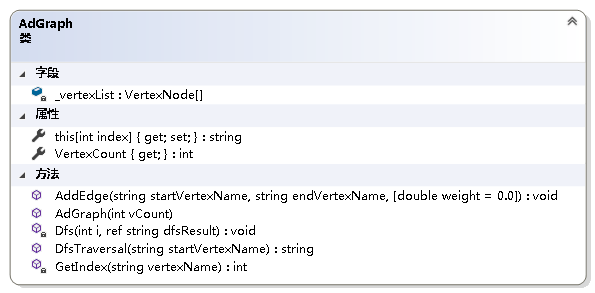
图22 AdGraph结构

private void Dfs(int i, ref string dfsResult){
       //深度优先搜索递归函数    _vertexList[i].Visited = true;    dfsResult += _vertexList[i].VertexName + "\n";    EdgeNode p = _vertexList[i].FirstNode;    while (p != null)    {
           if (_vertexList[p.Index].Visited)            p = p.Next;        else            Dfs(p.Index, ref dfsResult);    }}/// /// 得到深度优先搜索序列/// 
/// 进行深度优先搜索的起始点名称/// 
   
    深度优先搜索序列
   public string DfsTraversal(string startVertexName){
       string dfsResult = string.Empty;    int i = GetIndex(startVertexName);    if (i != -1)    {
           for (int j = 0; j < VertexCount; j++)            _vertexList[j].Visited = false;        Dfs(i, ref dfsResult);    }    return dfsResult;}

3.2 广度优先搜索

算法：

假设 $G = (V, E)$ 以 $S$ 为起点（源点）进行搜索。

首先标识 $S$ 为已访问结点，接着访问 $S$ 的邻接点 $\omega_1,\omega_2,\cdots,\omega_t$ 然后访问 $\omega_1,\omega_2,\cdots,\omega_t$ 的未被访问的邻接点，以此类推，直到与 $S$ 有路径相连的所有结点都被访问到。

先来先服务的思想。

例子：

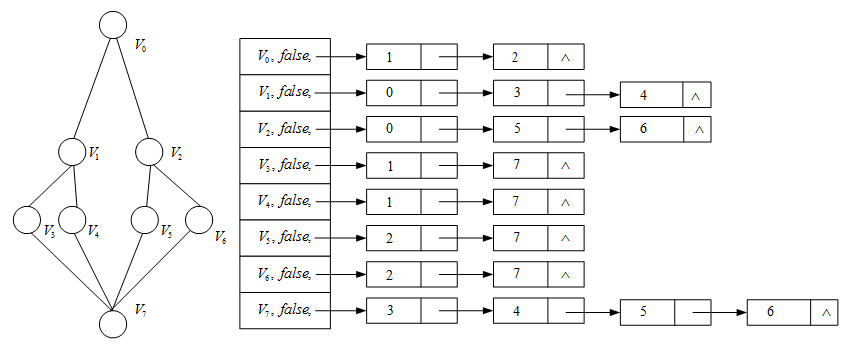
图23 图的结构

深度优先搜索的序列为： $V_0,V_1,V_2,V_3,V_4,V_5,V_6,V_7$

虽然遍历序列不唯一，但是邻接表确定后，遍历序列就唯一了。

实现：

图24 AdGraph结构

/// /// 得到广度优先搜索序列/// 
/// 进行广度优先搜索的起始点名称/// 
   
    广度优先搜索序列
   public string BfsTraversal(string startNodeName){
       string bfsResult = string.Empty;    int i = GetIndex(startNodeName);    if (i != -1)    {
           for (int j = 0; j < VertexCount; j++)            _vertexList[j].Visited = false;        _vertexList[i].Visited = true;        bfsResult += _vertexList[i].VertexName + "\n";        LinkQueue
   
     lq = new LinkQueue
    
     ();        lq.EnQueue(i);        while (lq.IsEmpty() == false)        {
               int j = lq.QueueFront;            lq.DeQueue();            EdgeNode p = _vertexList[j].FirstNode;            while (p != null)            {
                   if (_vertexList[p.Index].Visited == false)                {
                       _vertexList[p.Index].Visited = true;                    bfsResult += _vertexList[p.Index].VertexName + "\n";                    lq.EnQueue(p.Index);                }                p = p.Next;            }        }    }    return bfsResult;}

4. 拓扑排序

4.1 基本概念

$A O V$ 网（Activity on Vertex Network）：用顶点表示活动，用有向边表示活动之间先后关系的有向图。

拓扑序列：把 $A O V$ 网中的所有顶点排成一个线性序列，使每个活动的所有前驱活动都排在该活动的前边。

拓扑排序：构造 $A O V$ 网拓扑序列的过程。

例题：按照拓扑排序安排下列课程

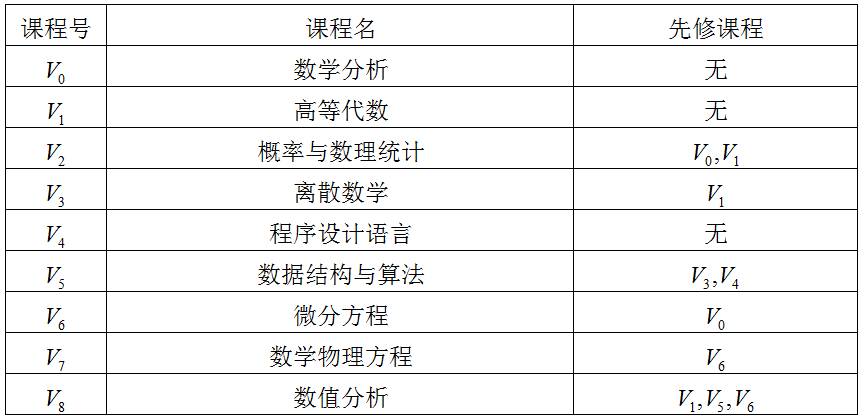
图25 课程表

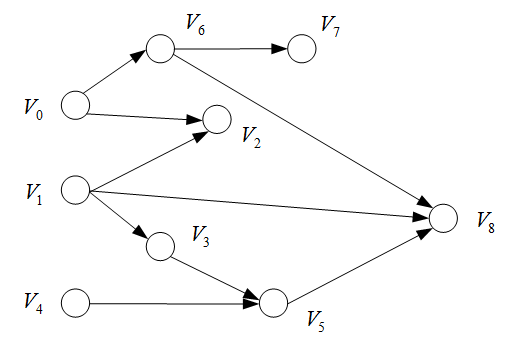
图26 AOV网

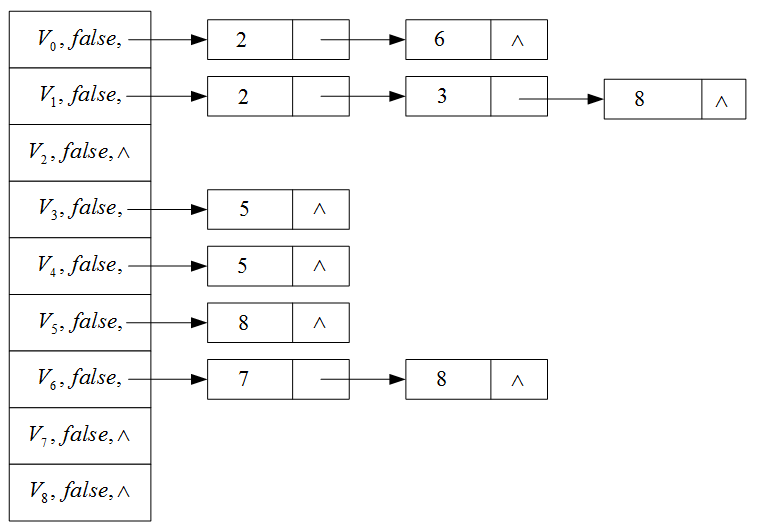
图27 AOV网的存储

4.2 算法步骤

第1步：从网中选择一个入度为0的顶点加入排序序列。

第2步：从网中删除该顶点及其所有出边。

第3步：执行第1、2步，直到所有顶点已排序或网中剩余顶点入度均不为0（说明：网中存在回路，无法继续拓扑排序）。

拓扑序列：

（1） $V_0,V_1,V_4,V_6,V_2,V_3,V_7,V_5,V_8$

（2） $V_0,V_6,V_1,V_2,V_3,V_4,V_5,V_8,V_7$

注：对于任何无回路的 $A O V$ 网，其顶点均可排成拓扑序列，但其拓扑序列未必唯一。

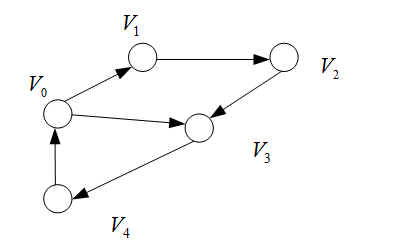
图28 存在回路的AOV网

存在回路的有向图，不能构成拓扑序列。

4.3 算法实现

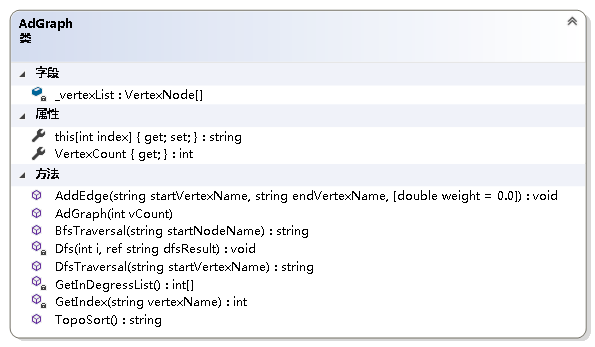
图29 AdGraph结构

/// /// 得到每个节点的入度/// 
/// 
   private int[] GetInDegressList(){
       int[] id = new int[VertexCount];    for (int i = 0; i < VertexCount; i++)    {
           EdgeNode p = _vertexList[i].FirstNode;        while (p != null)        {
               id[p.Index]++;            p = p.Next;        }    }    return id;}/// /// 得到AOV网的拓扑排序序列/// 
/// 
   
    AOV网的拓扑排序序列
   public string TopoSort(){
       string result = string.Empty;    int[] id = GetInDegressList();    LinkQueue
   
     lq = new LinkQueue
    
     ();    for (int i = 0; i < VertexCount; i++)    {
           if (id[i] == 0)            lq.EnQueue(i);    }    if (lq.Length == VertexCount)        throw new Exception("此有向图无有向边.");    while (lq.IsEmpty() == false)    {
           int j = lq.QueueFront;        lq.DeQueue();        result += _vertexList[j].VertexName + "\n";        EdgeNode p = _vertexList[j].FirstNode;        while (p != null)        {
               id[p.Index]--;            if (id[p.Index] == 0)            {
                   lq.EnQueue(p.Index);            }            p = p.Next;        }    }    int k;    for (k = 0; k < VertexCount; k++)    {
           if (id[k] != 0)        {
               break;        }    }    return (k == VertexCount) ? result : "该AOV网有环.";}

5. 最小生成树

5.1 基本概念

生成树：设 $G$ 为连通网，具有 $G$ 的所有顶点（ $n$ 个）且只有 $n - 1$ 条边的连通子网。

树的权：生成树 $T$ 的各边的权值总和。

最小生成树：权值最小的生成树。

5.2 Prim算法

算法原理（贪心算法）：

设 $G = (V, E)$ 为连通网， $T = (U, T E)$ 为其对应的最小生成树，从 $v_0$ 开始构造。

（1）开始时， $\lbrace u_0=v_0 \rbrace$

u0=v0}，

TE=\Phi

。

（2）找到满足 $\lbrace weight(u_i,v_j)|u_i \in U,v_j\in V-U \rbrace$

weight(ui,vj)∣ui∈U,vj∈V−U}的边，把它并入

T E

中，

v

同时并入

U

。

（3）反复执行（2），直到 $U = V$ 时，终止算法。

例题：

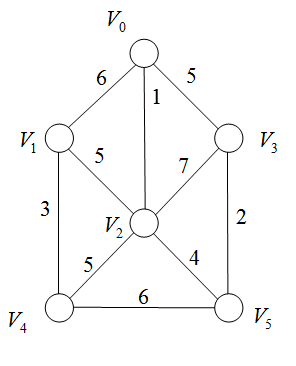
图30 连通图

图31 连通图的存储

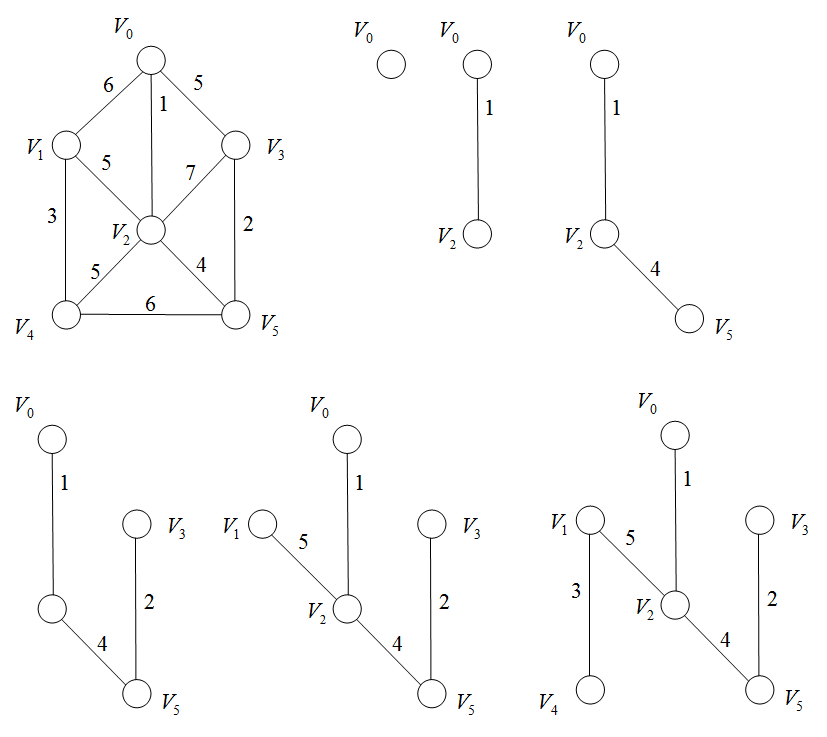
图32 最小生成树的构建

算法实现：

最小生成树结点的存储：

图33 最小生成树结点的结构

图34 SpanTreeNode结构

using System;namespace NonLinearStruct{
       ///     /// 生成树结点的抽象数据类型    /// 
    public class SpanTreeNode    {
           ///         /// 获取或设置结点本身的名称        /// 
        public string SelfName {
    get; }        ///         /// 获取或设置结点双亲的名称        /// 
        public string ParentName {
    get; }        ///         /// 获取或设置边的权值        /// 
        public double Weight {
    get; set; }        ///         /// 构造SpanTreeNode实例        /// 
        /// 结点本身的名称        /// 结点双亲的名称        /// 边的权值        public SpanTreeNode(string selfName, string parentName, double weight)        {
               if (string.IsNullOrEmpty(selfName) || string.IsNullOrEmpty(parentName))                throw new ArgumentNullException();            SelfName = selfName;            ParentName = parentName;            Weight = weight;        }    }}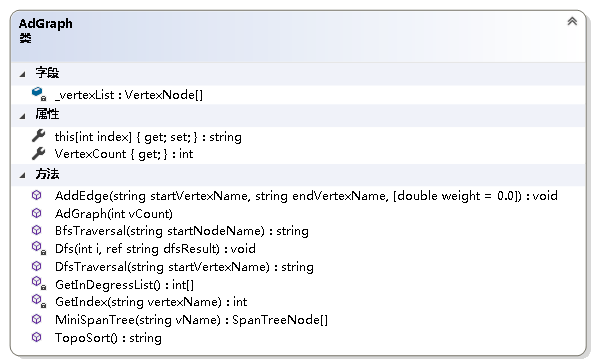

图35 AdGraph结构

/// /// 得到连通网的最小生成树Prim算法/// 
/// 树根结点/// 
   
    连通网的最小生成树
   public SpanTreeNode[] MiniSpanTree(string vName){
       int i = GetIndex(vName);    if (i == -1)        return null;    SpanTreeNode[] spanTree = new SpanTreeNode[VertexCount];    spanTree[0] = new SpanTreeNode(_vertexList[i].VertexName, "NULL", 0.0);    //U中结点到各结点最小权值那个结点在VertexList中的索引号    int[] vertexIndex = new int[VertexCount];    //U中结点到各个结点的最小权值    double[] lowCost = new double[VertexCount];    for (int j = 0; j < VertexCount; j++)    {
           lowCost[j] = double.MaxValue;        vertexIndex[j] = i;    }    EdgeNode p1 = _vertexList[i].FirstNode;    while (p1 != null)    {
           lowCost[p1.Index] = p1.Weight;        p1 = p1.Next;    }    vertexIndex[i] = -1;    for (int count = 1; count < VertexCount; count++)    {
           double min = double.MaxValue;        int v = i;        for (int k = 0; k < VertexCount; k++)        {
               if (vertexIndex[k] != -1 && lowCost[k] < min)            {
                   min = lowCost[k];                v = k;            }        }        spanTree[count] = new SpanTreeNode(_vertexList[v].VertexName, _vertexList[vertexIndex[v]].VertexName, min);        vertexIndex[v] = -1;        EdgeNode p2 = _vertexList[v].FirstNode;        while (p2 != null)        {
               if (vertexIndex[p2.Index] != -1 && p2.Weight < lowCost[p2.Index])            {
                   lowCost[p2.Index] = p2.Weight;                vertexIndex[p2.Index] = v;            }            p2 = p2.Next;        }    }    return spanTree;}

5.3 Kruskar算法

设 $G = (V, E)$ 为连通网， $T$ 为其对应的最小生成树。

（1）初始时 $T=\lbrace V, \lbrace \Phi \rbrace \rbrace$

V,{

Φ}}，即

T

中没有边，只有

n

个顶点，就是

n

个连通分量。

（2）在 $E$ 中选择权值最小的边 $(u, v)$ ，并将此边从 $E$ 中删除。

（3）如果 $u$ ， $v$ 在 $T$ 的不同的连通分量中，则将 $(u, v)$ 加入到 $T$ 中，从而导致 $T$ 中减少一个连通分量。

（4）反复执行（2）（3）直到 $T$ 中仅剩一个连通分量时，终止操作。

例题：

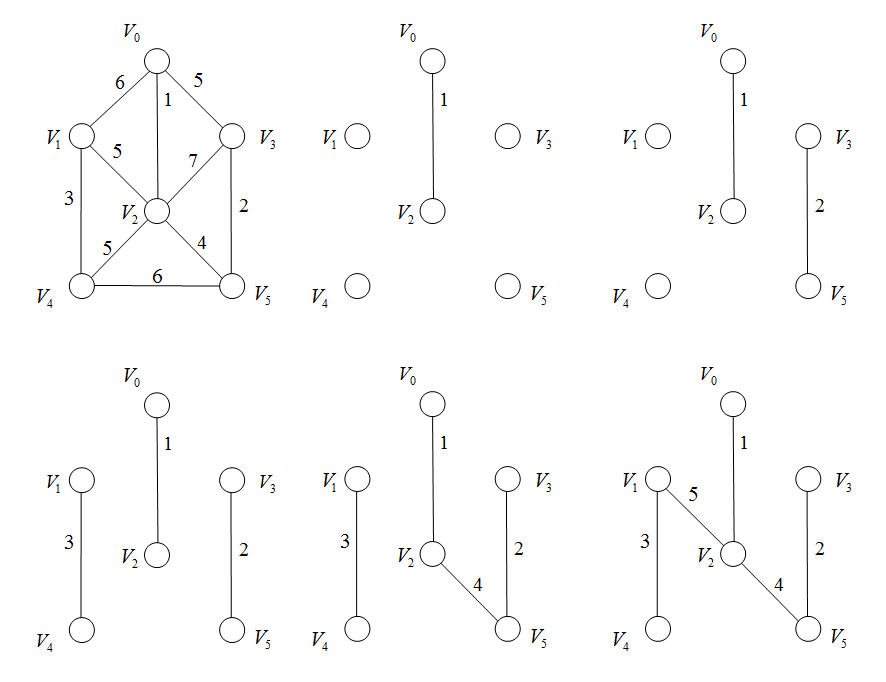
图36 最小生成树的构建

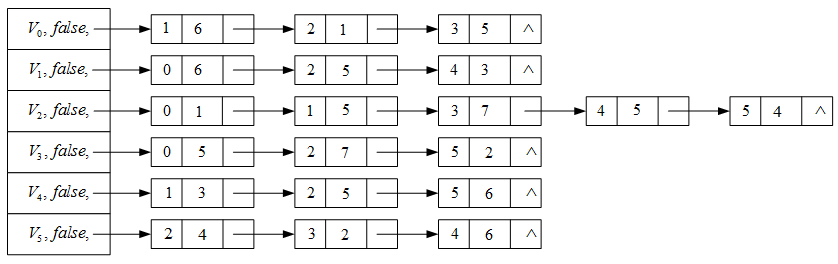
图37 连通图的存储

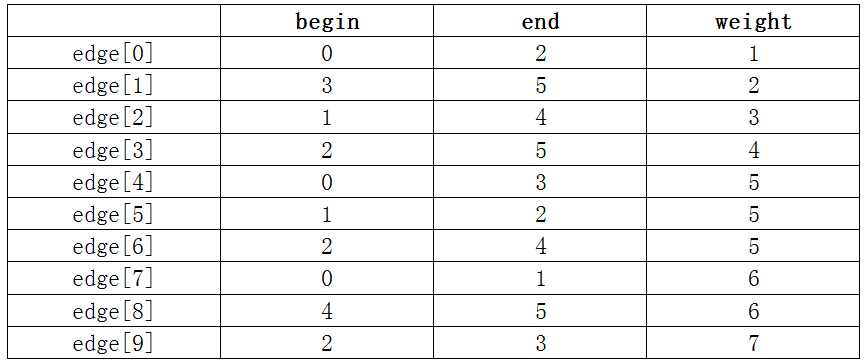
图38 边的集合

算法实现：

图39 Edge结构

namespace NonLinearStruct.Graph{
       ///     /// 表示图的边    /// 
    public class Edge    {
           ///         /// 起点编号        /// 
        public int Begin {
    get; }        ///         /// 终点编号        /// 
        public int End {
    get; }        ///         /// 权值        /// 
        public double Weight {
    get; }        ///         /// 创建一个 Edge 类的新实例        /// 
        /// 起点编号        /// 终点编号        /// 权值        public Edge(int begin, int end, double weight = 0.0)        {
               Begin = begin;            End = end;            Weight = weight;        }    }}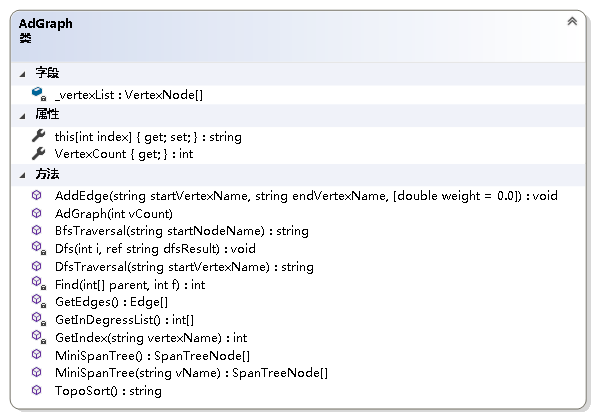

图40 AdGraph结构

private Edge[] GetEdges(){
       for (int i = 0; i < VertexCount; i++)        _vertexList[i].Visited = false;    List
   
     result = new List
    
     ();        for (int i = 0; i < VertexCount; i++)    {
           _vertexList[i].Visited = true;        EdgeNode p = _vertexList[i].FirstNode;        while (p != null)        {
               if (_vertexList[p.Index].Visited == false)            {
                   Edge edge = new Edge(i, p.Index, p.Weight);                result.Add(edge);            }            p = p.Next;        }    }    return result.OrderBy(a => a.Weight).ToArray();}private int Find(int[] parent, int f){
       while (parent[f] > -1)        f = parent[f];    return f;}/// 
     /// 克鲁斯卡尔算法 最小生成树/// 
/// 
     public SpanTreeNode[] MiniSpanTree(){
       int[] parent = new int[VertexCount];    for (int i = 0; i < VertexCount; i++)    {
           parent[i] = -1;    }    SpanTreeNode[] tree = new SpanTreeNode[VertexCount];    Edge[] edges = GetEdges();    int count = 1;    for (int i = 0; i < edges.Length; i++)    {
           int begin = edges[i].Begin;        int end = edges[i].End;        int b = Find(parent, begin);        int e = Find(parent, end);        if (b != e)        {
               parent[e] = b;            tree[count] = new SpanTreeNode(_vertexList[end].VertexName,                _vertexList[begin].VertexName, edges[i].Weight);            count++;        }    }    for (int i = 0; i < parent.Length; i++)    {
           if (parent[i] == -1)        {
               tree[0] = new SpanTreeNode(_vertexList[i].VertexName, "NULL", 0.0);            break;        }    }    return tree;}

6. 单源最短路径

6.1 定义

设 $G = (V, E)$ 为连通网， $v$ 为源点， $v$ 到其余各顶点的最短路径问题即为单源最短路径问题。

6.2 迪杰特撕拉算法

$D i j k s t r a$ （迪杰特斯拉）算法（按路径长度递增顺序构造的算法）：

初始时 $s$ 为源点， $D_s=0$ ， $D_i= + \infty (i \neq s)$ ，标识 $s$ 被访问。

（1）令 $v = s$ ， $D_v=0$ （ $v$ 到 $s$ 的路径长度）。

（2）依次考察 $v$ 的未被访问的邻接点 $\omega$ ，若 $D_v+weight(v,\omega)<D_\omega$ ，则改变 $D_\omega$ 的值，使 $D_\omega=D_v+weight(v,\omega)$ 。

（3）在未被访问顶点中选择 $D_v$ 最小的顶点 $v$ ，访问 $v$ 。

（4）重复（2）、（3）直至所有顶点都被访问。

例题：

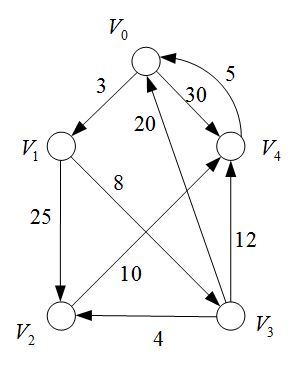
图41 原始图

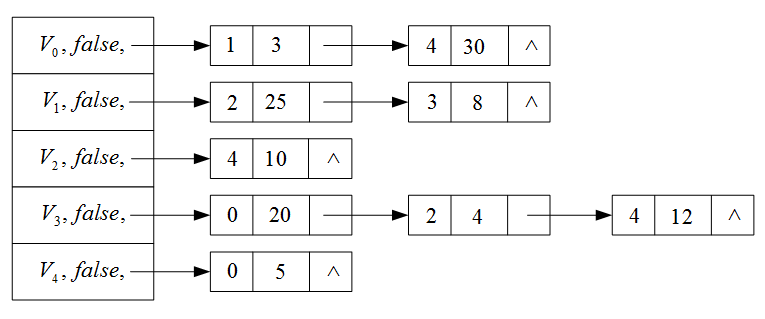
图42 图的存储结构

图43 最短路径结果

算法实现：

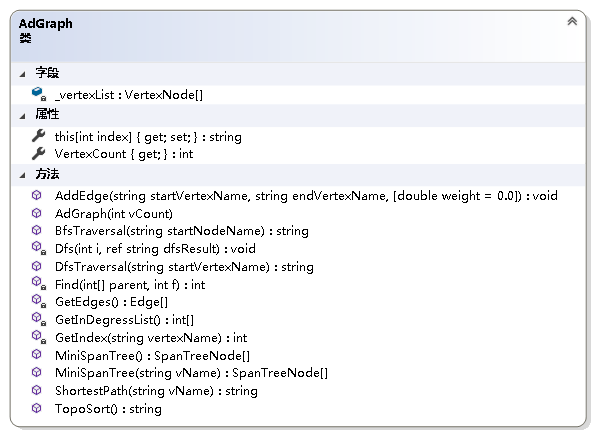
图44 AdGraph结构

/// /// 单源最短路径/// 
/// 寻找最短路径的源点/// 
   
    源点到各个顶点的最短路径
   public string ShortestPath(string vName){
       int v = GetIndex(vName);    if (v == -1)    {
           return string.Empty;    }    string result = string.Empty;    double[] dist = new double[VertexCount];    string[] path = new string[VertexCount];    //初始化    for (int i = 0; i < VertexCount; i++)    {
           _vertexList[i].Visited = false;        dist[i] = double.MaxValue;        path[i] = _vertexList[v].VertexName;    }    dist[v] = 0.0;    _vertexList[v].Visited = true;    for (int i = 0; i < VertexCount - 1; i++)    {
           EdgeNode p = _vertexList[v].FirstNode;        while (p != null)        {
               if (_vertexList[p.Index].Visited == false                && dist[v] + p.Weight < dist[p.Index])            {
                   dist[p.Index] = dist[v] + p.Weight;                path[p.Index] = path[v] + " ->" + _vertexList[p.Index].VertexName;            }            p = p.Next;        }        double min = double.MaxValue;        for (int j = 0; j < VertexCount; j++)        {
               if (_vertexList[j].Visited == false && dist[j] < min)            {
                   min = dist[j];                v = j;            }        }        _vertexList[v].Visited = true;    }    for (int i = 0; i < VertexCount; i++)    {
           result += path[i] + ":" + dist[i] + "\n";    }    return result;}

7. 连通分量

例题：

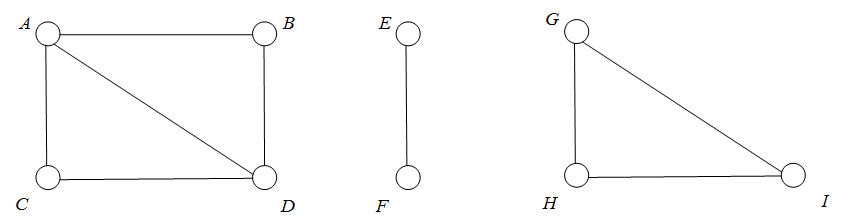
图45 原始图

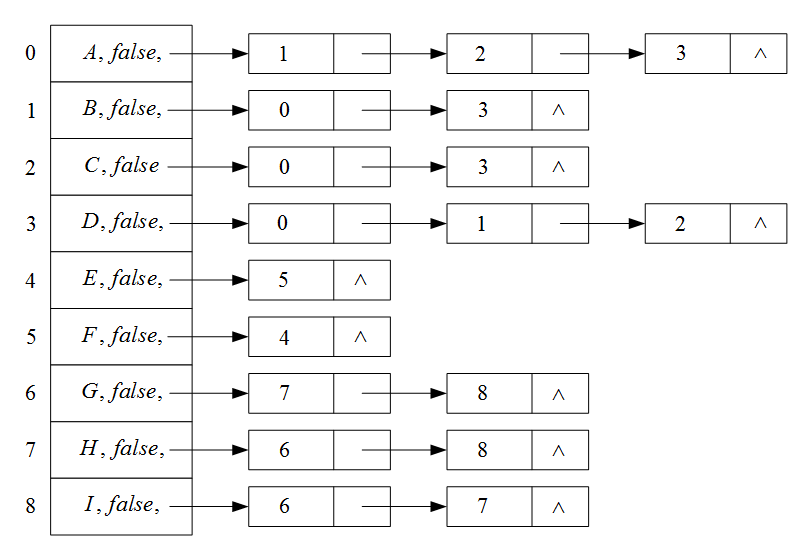
图46 图的存储结构

可利用深度优先搜索，求非连通图的连通分量。

第一个：A，B，D，C；第二个：E，F；第三个：G，H，I

算法实现：

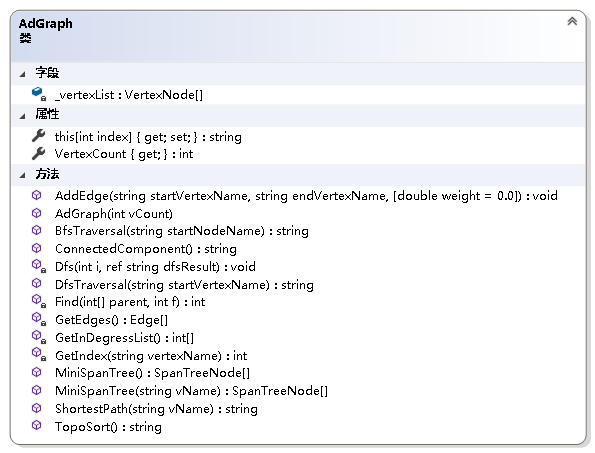
图47 AdGraph结构

/// /// 得到连通分量/// 
/// 
   
    连通分量
   public string ConnectedComponent(){
       string result;    SLinkList
   
     lst = new SLinkList
    
     ();    for (int i = 0; i < VertexCount; i++)        _vertexList[i].Visited = false;    for (int i = 0; i < VertexCount; i++)    {
           if (_vertexList[i].Visited == false)        {
               result = string.Empty;            //利用深度优先搜索求非连通图的连通分量            Dfs(i, ref result);            lst.InsertAtRear(result);        }    }    result = string.Empty;    for (int i = 0; i < lst.Length; i++)    {
           result += "第" + i + "个连通分量为:\n" + lst[i];    }    return result;}

8. 练习

根据要求完成程序代码：

给定纽约市附近的一幅简单地图，图中的顶点为城市，无向边代表两个城市的连通关系，边上的权为两城市之间的距离。

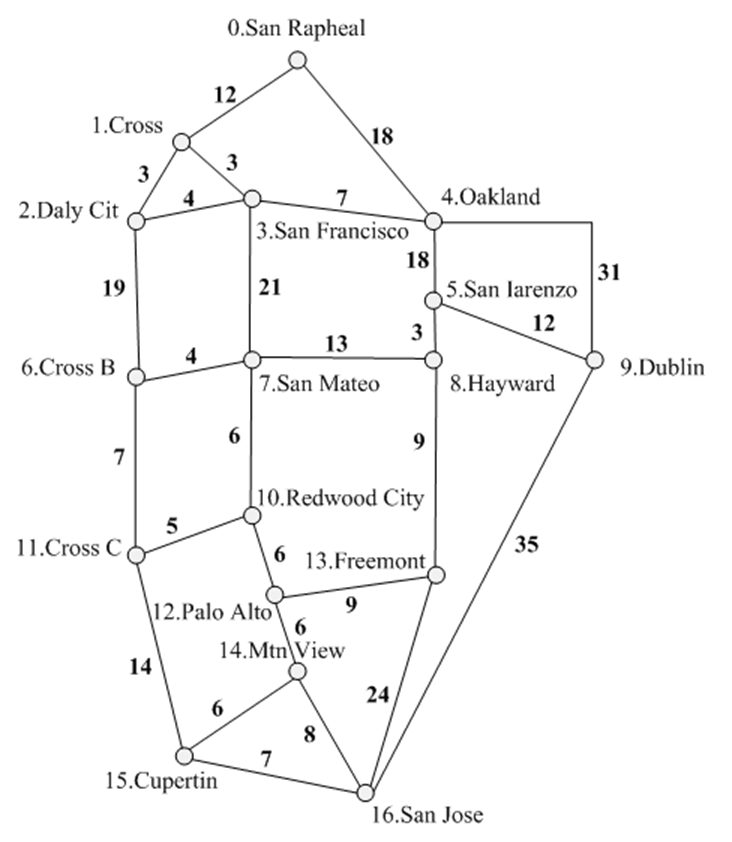
图48 纽约市附近地图

（1）对该图进行深度优先和广度优先搜索，并输出搜索序列（图的搜索问题）。

（2）在分析这张图后可以发现，任一对城市都是连通的。

第一个问题是：要用公路把所有城市连接起来，如何设计可使得工程的总造价最少（最小生成树问题）。

第二个问题是：要开车从一个城市到另外一个城市求其最短距离以及驱车路线（最短路径问题）。

解答：

数据TXT文件：

Source,Target,WeightSan Rapheal,Cross,12San Rapheal,Oakland,18Cross,Daly Cit,3Cross,San Franciso,3Daly Cit,San Franciso,4Daly Cit,Cross B,19San Franciso,Oakland,7San Franciso,San Mateo,21Oakland,San Iarenzo,18Oakland,Dublin,31San Iarenzo,Hayward,3San Iarenzo,Dublin,12Cross B,San Mateo,4Cross B,Cross C,7San Mateo,Hayward,13San Mateo,Redwood City,6Hayward,Freemont,9Dublin,San Jose,35Redwood City,Cross C,5Redwood City,Palo Alto,6Cross C,Cupertin,14Palo Alto,Freemont,9Palo Alto,Mtn View,6Freemont,San Jose,24Mtn View,Cupertin,6Mtn View,San Jose,8Cupertin,San Jose,7

深度优先搜索序列：

San RaphealCrossDaly CitSan FrancisoOaklandSan IarenzoHaywardSan MateoCross BCross CRedwood CityPalo AltoFreemontSan JoseDublinMtn ViewCupertin

广度优先搜索序列：

San RaphealCrossOaklandDaly CitSan FrancisoSan IarenzoDublinCross BSan MateoHaywardSan JoseCross CRedwood CityFreemontMtn ViewCupertinPalo Alto

最小生成树：

(NULL,San Rapheal) Weight:0(San Rapheal,Cross) Weight:12(Cross,Daly Cit) Weight:3(Cross,San Franciso) Weight:3(San Franciso,Oakland) Weight:7(Oakland,San Iarenzo) Weight:18(San Iarenzo,Hayward) Weight:3(Hayward,Freemont) Weight:9(Freemont,Palo Alto) Weight:9(Palo Alto,Redwood City) Weight:6(Redwood City,Cross C) Weight:5(Redwood City,San Mateo) Weight:6(San Mateo,Cross B) Weight:4(Palo Alto,Mtn View) Weight:6(Mtn View,Cupertin) Weight:6(Cupertin,San Jose) Weight:7(San Iarenzo,Dublin) Weight:12最小生成树权值：116

最短路径：

San Rapheal:0San Rapheal ->Cross:12San Rapheal ->Oakland:18San Rapheal ->Cross ->Daly Cit:15San Rapheal ->Cross ->San Franciso:15San Rapheal ->Cross ->Daly Cit ->Cross B:34San Rapheal ->Cross ->San Franciso ->San Mateo:36San Rapheal ->Oakland ->San Iarenzo:36San Rapheal ->Oakland ->San Iarenzo ->Dublin:48San Rapheal ->Oakland ->San Iarenzo ->Hayward:39San Rapheal ->Cross ->Daly Cit ->Cross B ->Cross C:41San Rapheal ->Cross ->San Franciso ->San Mateo ->Redwood City:42San Rapheal ->Oakland ->San Iarenzo ->Hayward ->Freemont:48San Rapheal ->Cross ->San Franciso ->San Mateo ->Redwood City ->Palo Alto ->Mtn View ->San Jose:62San Rapheal ->Cross ->San Franciso ->San Mateo ->Redwood City ->Palo Alto:48San Rapheal ->Cross ->Daly Cit ->Cross B ->Cross C ->Cupertin:55San Rapheal ->Cross ->San Franciso ->San Mateo ->Redwood City ->Palo Alto ->Mtn View:54

转载地址：https://lsgogroup.blog.csdn.net/article/details/109556856 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！

上一篇：技术图文：03 结构型设计模式（上）

下一篇：线性代数：第二章矩阵及其运算

发表评论

关于作者

喝酒易醉，品茶养心，人生如梦，品茶悟道，何以解忧？唯有杜康！

-- 愿君每日到此一游！

17 图

1. 图的基本概念与术语

1.1 图的定义

1.2 图的分类

1.3 图中顶点数与边数的关系

1.4 路径

1.5 子图

1.6 连通图与连通分量（无向图）

1.7 强连通图与强连通分量（有向图）

1.8 网络

2. 图的存储结构

2.1 顺序存储（邻接矩阵）

2.2 链式存储（邻接表）

3. 图的遍历

3.1 深度优先搜索

3.2 广度优先搜索

4. 拓扑排序

4.1 基本概念

4.2 算法步骤

4.3 算法实现

5. 最小生成树

5.1 基本概念

5.2 Prim算法

5.3 Kruskar算法

6. 单源最短路径

6.1 定义

6.2 迪杰特撕拉算法

7. 连通分量

8. 练习

发表评论

最新留言

关于作者

推荐文章